Question

（本题满分12分）

已知f (x)＝sinx＋cosx (xÎR)．

（Ⅰ）求函数f (x)的周期和最大值； 

（Ⅱ）若f (A＋)＝，求cos2A的值．

 

Answer 1

【答案】

(Ⅰ) x＝2kp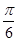＋ (kÎZ)，f (x)的最大值为2．（Ⅱ）－．

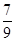【解析】

试题分析：(Ⅰ) f (x)＝2sin(x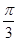＋)，∴最小正周期T＝2p．……3分

当x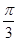＋＝2kp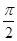＋时，即x＝2kp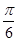＋ (kÎZ)，f (x)的最大值为2．……6分

（Ⅱ）f (A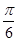＋)＝2sin(A+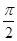)＝2cosA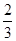＝，∴cosA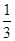＝．……9分

cos2A＝2cos²A-1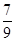＝－．……12分

考点：本题主要考查三角函数诱导公式，三角函数和差倍半公式，三角函数的性质。

点评：典型题，在利用三角函数恒等变换解题过程中，“变角、变号、变名”是常用技巧，为研究三角函数的性质，往往要先将函数“化一”。（2）小题首先求得cosA，利用倍角公式求得cos2A。