题目内容
在圆x2+y2=5x内,过点( ,
, )有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差d∈[
)有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差d∈[ ,
, ],那么n的取值集合为( )
],那么n的取值集合为( )A.{4,5,6,7}
B.{4,5,6}
C.{3,4,5,6}
D.{3,4,5}
【答案】分析:先求出圆的圆心和半径,根据圆的几何性质计算出过点 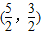 的最短弦长和最长弦长,即等差数列的第一项和第n项,再根据等差数列的公差d∈[
的最短弦长和最长弦长,即等差数列的第一项和第n项,再根据等差数列的公差d∈[ ,
, ],求出n的取值集合.
],求出n的取值集合.
解答:解:圆x2+y2=5x的圆心为C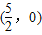 ,半径为r=
,半径为r=
过点P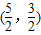 最短弦的弦长为a1=2
最短弦的弦长为a1=2 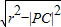 =4
=4
过点P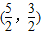 最长弦长为圆的直径长an=5,
最长弦长为圆的直径长an=5,
∴4+(n-1)d=5,
d=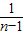 ,
,
∵d∈[ ,
, ],
],
∴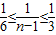 ,
,
∴4≤n≤7.
故选A.
点评:本题考察了圆的方程,圆的几何性质及等差数列的通项公式等知识,解题时要学会使用圆的几何性质解决圆的弦长问题,提高解题速度.
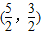 的最短弦长和最长弦长,即等差数列的第一项和第n项,再根据等差数列的公差d∈[
的最短弦长和最长弦长,即等差数列的第一项和第n项,再根据等差数列的公差d∈[ ,
, ],求出n的取值集合.
],求出n的取值集合.解答:解:圆x2+y2=5x的圆心为C
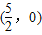 ,半径为r=
,半径为r=
过点P
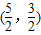 最短弦的弦长为a1=2
最短弦的弦长为a1=2 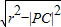 =4
=4过点P
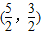 最长弦长为圆的直径长an=5,
最长弦长为圆的直径长an=5,∴4+(n-1)d=5,
d=
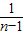 ,
,∵d∈[
 ,
, ],
],∴
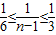 ,
,∴4≤n≤7.
故选A.
点评:本题考察了圆的方程,圆的几何性质及等差数列的通项公式等知识,解题时要学会使用圆的几何性质解决圆的弦长问题,提高解题速度.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目