Question

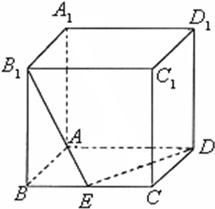如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，E是BC的中点，平面B₁ED交A₁D₁于F
（1）指出F在A₁D₁上的位置，并证明；
（2）求三棱锥C₁-B₁EF的体积．

Answer 1

分析：作图后（1）F在A₁D₁上的中点；只需证明四边形B₁FDE为平行四边形，即可．
（2）利用等体积的思想转化为：求三棱锥C₁-B₁EF的体积，就是求F-B₁EC₁的体积．

解答：解：（1）F为A₁D₁上的中点．证明如下：取A₁D₁上的中点F，连接DF，ED，∵△B₁A₁F≌△DCE，△DD₁F≌△B₁BE∴B₁F=ED，B₁=FD∴四边形B₁FDE为平行四边形∴平面B₁ED交A₁D₁于A₁D₁的中点F
（2）VC1-B1EF=VF-B1EC1=

1

3

×

1

2

×1×1×1=

1

6

点评：本题考查直线与平面平行的性质，棱锥的体积，考查空间想象能力，是基础题．