题目内容
函数 的图像在点P(1,0)处的切线斜率为2.
的图像在点P(1,0)处的切线斜率为2.
(1)求a,b的值;(2)证明: 对任意正实数x恒成立。
对任意正实数x恒成立。
试题解析:由题设,y=f(x)在点P(1,0)处切线的斜率为2.
∴ 解之得
解之得 6分
6分
因此实数a,b的值分别为-1和3.
(2)证明  (x>0).
(x>0).
设g(x)=f(x)-(2x-2)=2-x- +3ln x,
+3ln x,
则g′(x)=-1-2x+ =-
=- .
.
当0<x<1时,g′(x)>0;当x>1时,g′(x)<0.
∴g(x)在 (0,1)上单调递增;在(1,+∞)上单调递减.
∴g(x)在x=1处有最大值g(1)=0,
∴f(x)-(2x-2)≤0,即f(x)≤2x-2,得证 12分
考点:利用导数研究函数切线及最值

练习册系列答案
相关题目
某校高三年级学生会主席团有共有5名同学组成,其中有3名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )
|
| A. | 0.35 | B. | 0.4 | C. | 0.6 | D. | 0.7 |
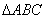 的边
的边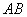 、
、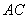 上分别取
上分别取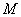 、
、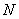 ,使
,使 ,
, ,
,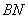 与
与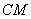 交于点
交于点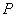 ,若
,若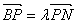 ,
,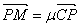 ,则
,则 .
. 的展开式中,
的展开式中, 项的系数是 .
项的系数是 .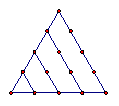 在古腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形
在古腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形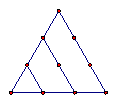
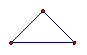
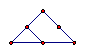

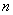 个三角形数为( )
个三角形数为( )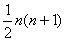 C.
C.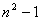 D.
D.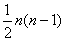
 是虚数单位,则
是虚数单位,则 等于
等于  满足
满足 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,则有( )
,则有( ) B.
B. C.
C. D.
D.

 B.
B.  C. 1 D. 6
C. 1 D. 6