题目内容
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)求出y关于x的线性回归方程![]() ;
;
(2)试预测加工10个零件需要多少小时?
(注:![]() =
= ,
,![]() =
=![]() -b
-b![]() )
)
【答案】(1)![]() =1.05+0.7x; (2)预测加工10个零件需要8.05小时.
=1.05+0.7x; (2)预测加工10个零件需要8.05小时.
【解析】
(1)先求均值,再根据公式求![]() 以及
以及![]() ,(2)在回归直线方程中令自变量为10,所得函数值为预测结果.
,(2)在回归直线方程中令自变量为10,所得函数值为预测结果.
(1)根据表中数据,计算![]() =
=![]() ×(2+3+4+5)=3.5,
×(2+3+4+5)=3.5,
![]() =
=![]() ×(2.5+3+4+4.5)=3.5,
×(2.5+3+4+4.5)=3.5,
![]() =
=![]() =0.7,
=0.7,
![]() =
=![]() -
-![]() =3.5-0.7×3.5=1.05,
=3.5-0.7×3.5=1.05,
∴y关于x的线性回归方程![]() =1.05+0.7x;
=1.05+0.7x;
(2)x=10时,计算![]() =1.05+0.7×10=8.05,
=1.05+0.7×10=8.05,
试预测加工10个零件需要8.05小时.

【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
【题目】大连市某企业为确定下一年投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中![]() ,
,![]() .
.
根据散点图判断,
![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
![]() 根据
根据![]() 的判断结果及表中数据,建立
的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
![]() 已知这种产品的年利润
已知这种产品的年利润![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据
.根据![]() 的结果回答下列问题:
的结果回答下列问题:
![]() 年宣传费
年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
![]() 年宣传费
年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
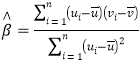 ,
,![]() .
.


