题目内容

设正2n+1(n∈N*)边形内接于一个圆，考虑所有以这2n+1边形的顶点为顶点的三角形，其中有多少个三角形的内部含该圆的圆心?

解析：如图，先取定一个顶点A，将其它2n个顶点顺次标为1，2，…，2n.

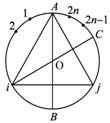
设以A，i(1≤i≤n)为一个端点的两条直径的另一个端点分别为B，C(注意：B，C不可能是正2n+1边形的顶点)，则上有i个顶点，这些顶点而且只有这些顶点与A，i构成锐角三角形.于是，以A，i(1≤i≤n)为顶点的锐角三角形有(个).因为A点有2n+1种取法，且在和(2n+1)×中每个三角形重复出三次，所以共有n=n(n+1)(2n+1)个

三角形内部含圆心O.

练习册系列答案
相关题目
对于数列{xn}，如果存在一个正整数m，使得对任意的n（n∈N*）都有xn+m=xn成立，那么就把这样一类数列{xn}称作周期为m的周期数列，m的最小值称作数列{xn}的最小正周期，以下简称周期．例如当xn=2时，{xn}是周期为1的周期数列，当yn=sin(
π
2
n)时，{yn}的周期为4的周期数列．
（1）设数列{an}满足an+2=λ•an+1-an（n∈N*），a1+a，a2=b（a，b不同时为0），且数列{an}是周期为3的周期数列，求常数λ的值；
（2）设数列{an}的前n项和为Sn，且4Sn=（an+1）2．
①若an＞0，试判断数列{an}是否为周期数列，并说明理由；
②若anan+1＜0，试判断数列{an}是否为周期数列，并说明理由．
（3）设数列{an}满足an+2=-an+1-an（n∈N*），a1=1，a2=2，bn=an+1，数列{bn}的前n项和Sn，试问是否存在p、q，使对任意的n∈N*都有p≤
Sn
n
≤q成立，若存在，求出p、q的取值范围；不存在，说明理由．
（2012•浦东新区一模）定义数列{xn}，如果存在常数p，使对任意正整数n，总有（xn+1-p）（xn-p）＜0成立，那么我们称数列{xn}为“p-摆动数列”．
（1）设an=2n-1，bn=(-
1
2
)n，n∈N*，判断{an}、{bn}是否为“p-摆动数列”，并说明理由；
（2）已知“p-摆动数列”{cn}满足cn+1=
1
cn+1
，c1=1，求常数p的值；
（3）设dn=（-1）n•（2n-1），且数列{dn}的前n项和为Sn，求证：数列{Sn}是“p-摆动数列”，并求出常数p的取值范围．
（2012•浦东新区一模）定义数列{xn}，如果存在常数p，使对任意正整数n，总有（xn+1-p）（xn-p）＜0成立，那么我们称数列{xn}为“p-摆动数列”．
（1）设an=2n-1，bn=(-
12
)n，n∈N*，判断{an}、{bn}是否为“p-摆动数列”，并说明理由；
（2）设数列{cn}为“p-摆动数列”，c1＞p，求证：对任意正整数m，n∈N*，总有c2n＜c2m-1成立；
（3）设数列{dn}的前n项和为Sn，且Sn=(-1)n•n，试问：数列{dn}是否为“p-摆动数列”，若是，求出p的取值范围；若不是，说明理由．
（2012•四川）已知a为正实数，n为自然数，抛物线y=-x2+
an
2
与x轴正半轴相交于点A，设f（n）为该抛物线在点A处的切线在y轴上的截距．
（Ⅰ）用a和n表示f（n）；
（Ⅱ）求对所有n都有
f(n)-1
f(n)+1
≥
n
n+1
成立的a的最小值；
（Ⅲ）当0＜a＜1时，比较
1
f(1)-f(2)
+
1
f(2)-f(4)
+…+
1
f(n)-f(2n)
与6•
f(1)-f(n+1)
f(0)-f(1)
的大小，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网