题目内容
若2x-1+4x+a=0有实数解,则实数a的取值范围是分析:先令b=2x,然后将方程2x-1+4x+a=0转化为一元二次方程b2+
+a=0,原方程有解等价于b2+
+a=0有正根,先对判别式进行判断求出a的范围,然后再由方程b2+
+a=0有正根进行排除即可.
| b |
| 2 |
| b |
| 2 |
| b |
| 2 |
解答:解:令b=2x>0,则b2+
+a=0,则方程要有正跟
首先△=
-4a≥0∴a≤
若a=
,则b2+
+
=0,即(b+
)2=0,没有正根,故不成立
当a<
时有两个不同的根
则b1+b2=-
,b1×b2=a
因为b1+b2<0,所以不可能两个根都是正的
必为一正一负
所以b1×b2=a<0
综上a<0
故答案为:(-∞,0).
| b |
| 2 |
首先△=
| 1 |
| 4 |
| 1 |
| 16 |
若a=
| 1 |
| 16 |
| b |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
当a<
| 1 |
| 16 |
则b1+b2=-
| 1 |
| 2 |
因为b1+b2<0,所以不可能两个根都是正的
必为一正一负
所以b1×b2=a<0
综上a<0
故答案为:(-∞,0).
点评:本题主要考查指数函数的值域与一元二次方程的根的判断.主要考查对基础知识的综合运用.

练习册系列答案
相关题目
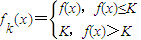 ,给出函数f(x)=2x+1-4x,若对于任意x∈(-∞,1],恒有fk(x)=f(x),则( )
,给出函数f(x)=2x+1-4x,若对于任意x∈(-∞,1],恒有fk(x)=f(x),则( )