题目内容
已知函数![]()
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
(1) ∴![]() ,
,![]() ,
,
(1)若![]() ,使
,使![]() 在(0,
在(0,![]() )上递增,在(
)上递增,在(![]() ,
,![]() )上递减,则
)上递减,则![]() ,
,
∴![]() ,这时
,这时![]() ,当
,当![]() 时,
时,![]() ,
,![]() 递增。
递增。
当![]() 时
时![]() ,
,![]() 递减。
递减。
(2)![]()
△=![]()
若△![]() ,即
,即![]() ,则
,则![]() 对
对![]() 恒成立,这时
恒成立,这时![]() 在
在![]() 上递减,∴
上递减,∴![]() 。
。
若![]() ,则当
,则当![]() 时,
时,![]() ,
, ,
,
![]() 不可能恒小于等于0。
不可能恒小于等于0。
若![]() ,则
,则 不合题意。
不合题意。
若![]() ,则
,则![]() ,
,![]() ,ks5u
,ks5u
∴![]() ,使
,使![]() ,
,
![]() 时,
时,![]() ,这时
,这时![]() 递增,
递增,![]() ,不合题意。
,不合题意。
综上![]() 。
。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
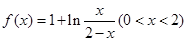 .
.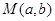 ,使得函数
,使得函数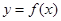 的图像上任意一点P关于点M对称的点Q也在函数
的图像上任意一点P关于点M对称的点Q也在函数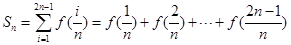 ,其中
,其中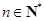 ,求
,求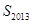 ;
;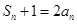 ,若不等式
,若不等式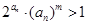 对
对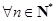 且
且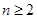 恒成立,求实数
恒成立,求实数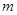 的取值范围.
的取值范围.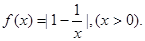
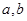
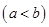 ,使得函数
,使得函数 的定义域、值域都是
的定义域、值域都是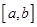 ,若存在,则求出
,若存在,则求出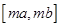 (
(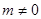 ),求
),求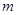 的取值范围.
的取值范围.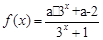 .
.
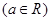
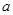 使函数f(x)为奇函数?证明你的结论;
使函数f(x)为奇函数?证明你的结论; .
.