题目内容
(本小题满分12分)设椭圆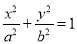 (a>b>0)的左右焦点分别为F1、F2,点D在椭圆上,DF1⊥F1F2,
(a>b>0)的左右焦点分别为F1、F2,点D在椭圆上,DF1⊥F1F2,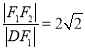 ,△DF1F2的面积为
,△DF1F2的面积为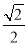 .
.
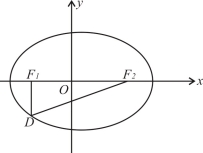
(1)求该椭圆的标准方程;
(2)若圆心在y轴上的圆与椭圆在x轴的上方有两个交点,且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点,求出这个圆的方程.
(1)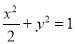 ;(2)x2+(y-
;(2)x2+(y-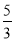 )2=
)2=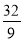 .
.
【解析】
试题分析:(1)由题设知F1(-c, 0),F2(c, 0)其中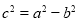 ,
,
由 ,结合条件△DF1F2的面积为
,结合条件△DF1F2的面积为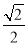 ,可求c的值,再利用椭圆的定义和勾股定理即可求得a,b的值,从而确定椭圆的标准方程;
,可求c的值,再利用椭圆的定义和勾股定理即可求得a,b的值,从而确定椭圆的标准方程;
(2)假设存在圆心在y轴上的圆,使圆在x轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点;设圆心在y轴上的圆与椭圆在x轴的上方有两个交点为A(x0, y0),B(-x0, y0)利用A(x0, y0),B(-x0, y0)在圆上及 确定交点的坐标,进而得到圆的方程.
确定交点的坐标,进而得到圆的方程.
试题解析:(1)设F1(-c, 0),F2(c, 0),|DF1|=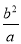 ,又
,又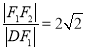 ,
,  ,
,
∴ ,∴a=
,∴a=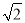 ,b=1,∴椭圆方形为
,b=1,∴椭圆方形为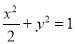 .
.
(2)设圆心在y轴上的圆与椭圆交于A(x0, y0),B(-x0, y0), F1A,F2B是圆C的两条切线,
F1(-1, 0),F2(1, 0),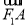 =(x0+1, y0),
=(x0+1, y0),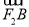 =(-x0-1, y0),
=(-x0-1, y0),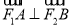 ,
,
∴-(x0+1)2+y02=0 即y02=(x0+1)2 ………………①
而 +y02=1 ………………②
+y02=1 ………………②
由①②得:
∴x0=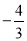 ,y0=
,y0=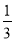 ,∴A(
,∴A(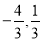 ),B(
),B(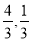 )
)
设圆心为C(0, m),则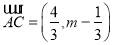 ,
,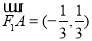 ,
,
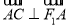 ,
,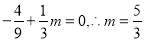 .
.
∴圆心C(0,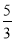 ),半径r =
),半径r = ,∴圆方程为x2+(y-
,∴圆方程为x2+(y-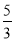 )2=
)2=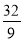 .
.
考点:圆的方程,直线雨啊椭圆的位置关系.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
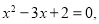 则
则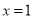 ”的逆否命题为“若
”的逆否命题为“若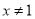 则
则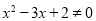 ”
”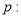 存在
存在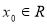 ,使得
,使得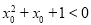 ,则非
,则非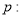 任意
任意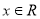 ,都有
,都有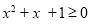
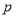 且
且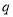 为假命题,则
为假命题,则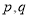 均为假命题
均为假命题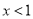 ”是“
”是“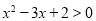 ”的充分不必要条件
”的充分不必要条件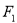 ,
,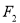 是双曲线
是双曲线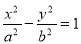
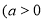 ,
,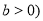 的左、右两个焦点,若双曲线右支上存在一点
的左、右两个焦点,若双曲线右支上存在一点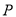 ,使
,使 (
(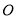 为坐标原点),且
为坐标原点),且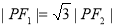 ,则双曲线的离心率为
,则双曲线的离心率为  B.
B.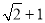 C.
C.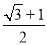 D.
D.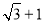
 ,则
,则 = .(结果用
= .(结果用 表示)
表示)
 在区间(0,1)内的零点个数是( )
在区间(0,1)内的零点个数是( )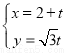 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为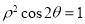 .
.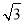 B.7+2
B.7+2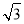 C.7+4
C.7+4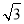 D.7-4
D.7-4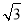
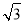 ,BC=1,AC=2,O为球心,则三棱锥O—ABC的体积为 .
,BC=1,AC=2,O为球心,则三棱锥O—ABC的体积为 .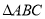 中,角
中,角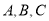 的对边分别为
的对边分别为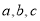 ,已知
,已知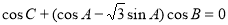 .
.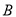 的大小;
的大小;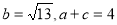 ,求△
,求△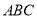 的面积.
的面积.