题目内容
在△ABC中,∠A=60°,a=4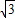 ,b=4
,b=4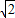 ,则B等于 .
,则B等于 .
【答案】分析:利用正弦定理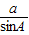 =
=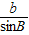 即可求得sinB,再由a>b知A>B,从而可得答案.
即可求得sinB,再由a>b知A>B,从而可得答案.
解答:解:∵在△ABC中,∠A=60°,a=4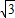 ,b=4
,b=4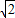 ,
,
∴由正弦定理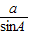 =
=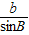 得:
得:
sinB=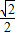 ,
,
又a=4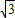 >b=4
>b=4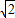 ,
,
∴60°=A>B,
∴B=45°.
故答案为:45°.
点评:本题考查正弦定理,在△ABC中,a>b知A>B是关键,属于基础题.
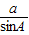 =
=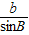 即可求得sinB,再由a>b知A>B,从而可得答案.
即可求得sinB,再由a>b知A>B,从而可得答案.解答:解:∵在△ABC中,∠A=60°,a=4
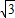 ,b=4
,b=4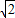 ,
,∴由正弦定理
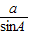 =
=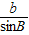 得:
得:sinB=
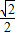 ,
,又a=4
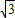 >b=4
>b=4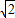 ,
,∴60°=A>B,
∴B=45°.
故答案为:45°.
点评:本题考查正弦定理,在△ABC中,a>b知A>B是关键,属于基础题.

练习册系列答案
相关题目