题目内容
【题目】已知直线![]() 且
且![]() .圆C与直线
.圆C与直线![]() 相切于点A,且点A的纵坐标为
相切于点A,且点A的纵坐标为![]() ,圆心C在直线
,圆心C在直线![]() 上.
上.
(1)求直线![]() 之间的距离;
之间的距离;
(2)求圆C的标准方程;
(3)若直线![]() 经过点
经过点![]() 且与圆C交于
且与圆C交于![]() 两点,当△CPQ的面积最大时,求直线
两点,当△CPQ的面积最大时,求直线![]() 的方程.
的方程.
【答案】(1)2(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)由两直线平等求得![]() ,然后由平行线间距离公式得距离.
,然后由平行线间距离公式得距离.
(2)求出![]() 点坐标,可得过
点坐标,可得过![]() 与
与![]() 垂直的直线方程,由此可得圆心坐标,得圆半径,从而得圆方程;
垂直的直线方程,由此可得圆心坐标,得圆半径,从而得圆方程;
(3)利用![]() 知
知![]() 时,面积最大.从而圆心到直线的距离为
时,面积最大.从而圆心到直线的距离为![]() ,从而求得直线方程.
,从而求得直线方程.
解:(1)∵两条线平行,
∴![]() ,
,
直线![]() 方程为
方程为![]() ,即
,即![]() ,
,
∴![]()
(2)∵![]()
由![]() 得
得![]() ,∴
,∴![]() ,
,
设过A与l2垂直的直线方程为![]() ,
,![]() ,
,![]() ,
,
∴过A与l2垂直的直线方程为![]() ,
,
∴![]() ,∴圆心为(0,0),半径为
,∴圆心为(0,0),半径为![]() ,
,
∴圆C的标准方程为![]()
(3)∵![]() ,
,
∴当![]() ,即
,即![]() 时,面积最大.此时,圆心到直线的距离为
时,面积最大.此时,圆心到直线的距离为![]() ,
,
显然直线![]() 满足题意,
满足题意,
当直线![]() 斜率存在时,设方程为
斜率存在时,设方程为![]() ,即
,即![]() ,
,
由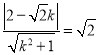 ,解得
,解得![]() ,直线方程为
,直线方程为![]() ,即
,即![]() .
.
∴直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目




