题目内容
(12分)已知过点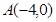 的动直线
的动直线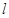 与抛物线
与抛物线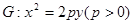 相交于
相交于 两点,当直线
两点,当直线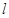 的斜率是
的斜率是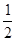 时,
时,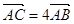 。
。
(1)求抛物线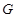 的方程;(5分)
的方程;(5分)
(2)设线段 的中垂线在
的中垂线在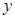 轴上的截距为
轴上的截距为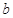 ,求
,求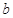 的取值范围。(7分)
的取值范围。(7分)
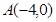 的动直线
的动直线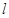 与抛物线
与抛物线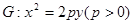 相交于
相交于 两点,当直线
两点,当直线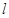 的斜率是
的斜率是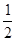 时,
时,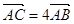 。
。(1)求抛物线
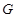 的方程;(5分)
的方程;(5分)(2)设线段
 的中垂线在
的中垂线在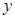 轴上的截距为
轴上的截距为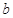 ,求
,求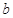 的取值范围。(7分)
的取值范围。(7分)(1) (2)
(2)
 (2)
(2)
试题分析:(1)设
 ,当直线
,当直线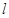 的斜率是
的斜率是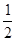 时,
时,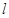 的方程为
的方程为 ,
,即
 ,由
,由 得
得 ,
, ,又
,又 ,由这三个表达式及
,由这三个表达式及 得
得 ,则抛物线的方程为
,则抛物线的方程为
(2)设
 的中点坐标为
的中点坐标为
由
 得
得
 ,
, 线段
线段 的中垂线方程为
的中垂线方程为 ,
, 线段
线段 的中垂线在
的中垂线在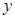 轴上的截距为:
轴上的截距为: ,由
,由 得
得 或
或

点评:本题中向量转化为点的坐标,用纵坐标y值比较简单

练习册系列答案
相关题目
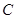 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上,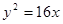 的准线交于
的准线交于 两点,
两点, ;则
;则 +
+ +
+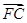 =0,则|
=0,则| 、
、 分别是圆
分别是圆 和椭圆
和椭圆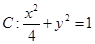 的弦,且弦的端点在
的弦,且弦的端点在 轴的异侧,端点
轴的异侧,端点 与
与 、
、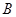 与
与 的横坐标分别相等,纵坐标分别同号.
的横坐标分别相等,纵坐标分别同号.
 ,且弦
,且弦 ,求直线
,求直线 ,试探究弦
,试探究弦 ,离心率为0.6,求椭圆的标准方程。
,离心率为0.6,求椭圆的标准方程。 的左、右两焦点分别为
的左、右两焦点分别为 ,点
,点 在椭圆上,
在椭圆上,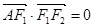 ,
, ,则椭圆的离心率
,则椭圆的离心率 等于 ( )
等于 ( )



 轴的距离少1.
轴的距离少1. 于
于 点,且
点,且 ,
, ,
, 的值。
的值。 有相同的焦点,直线y=
有相同的焦点,直线y=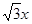 为
为 的一条渐近线.
的一条渐近线.  (0,4)的直线
(0,4)的直线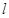 ,交双曲线
,交双曲线 点(
点( =
=
 ,且
,且 时,求
时,求 、
、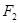 是双曲线
是双曲线 的两焦点,点
的两焦点,点 在该双曲线上,且
在该双曲线上,且 是等腰三角形,则
是等腰三角形,则


