题目内容
若直线l与直线x-3y+10=0交于点M，与直线2x+y-8=0交于点N，MN的中点为P（0，1），则直线l的方程是（ ）
| A、x+4y+4=0 | B、x+4y-4=0 | C、x-4y+4=0 | D、x-4y-4=0 |
分析：设出M的坐标，根据中点坐标公式得到N的坐标，然后分别把M、N代入到两方程中得到关于a和b的二元一次方程组，求出a、b即可得到M与N的坐标，利用两点式得到直线方程，化为一般式即可．
解答：解：设M（a，b），根据P（0，1）为两交点的中点得到N（-a，2-b），
把M代入x-3y+10=0得到a-3b+10=0①；把N代入2x+y-8=0得到-2a+2-b-8=0即2a+b+6=0②
联立①②得：
，
解得
，
所以M（-4，2），N（4，0）
则直线l的方程为：y-0=
（x-4），
化简为：x+4y-4=0．
故选B
把M代入x-3y+10=0得到a-3b+10=0①；把N代入2x+y-8=0得到-2a+2-b-8=0即2a+b+6=0②
联立①②得：
|
解得
|
所以M（-4，2），N（4，0）
则直线l的方程为：y-0=
| 0-2 |
| 4+4 |
化简为：x+4y-4=0．
故选B
点评：考查学生灵活运用中点坐标公式化简求值，会根据两点坐标求直线方程．理解两直线交点的意义．
练习册系列答案
名校课堂系列答案
相关题目
若曲线y=x4的一条切线l与直线x+4y-8=0垂直，则l的方程为（ ）
| A、4x-y-3=0 | B、x+4y-5=0 | C、4x-y+3=0 | D、x+4y+3=0 |
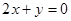上，并经过A
，
两点。
，从圆C外一点P(x，y)向圆引一条切线，切点为M. 且有|PM|＝|PD|，求使得|PM|取得最小值的点P的坐标. 
，且直线l不过第四象限．
+
的最小值．