题目内容
已知向量 ,函数
,函数 ,
, .
.
(1)求f(x)的最小值和单调区间;
(2)若 ,求sin2α的值.
,求sin2α的值.
 ,函数
,函数 ,
, .
.(1)求f(x)的最小值和单调区间;
(2)若
 ,求sin2α的值.
,求sin2α的值.解: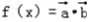 =sin2x+sinxcosx
=sin2x+sinxcosx
=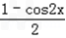 +
+ sin2x=
sin2x= (sin2x﹣cos2x)+
(sin2x﹣cos2x)+
=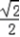 sin(2x﹣
sin(2x﹣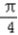 )+
)+ (1)
(1)
∵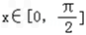 ,∴2x﹣
,∴2x﹣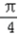 ∈[﹣
∈[﹣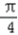 ,
, ]
]
∵当2x﹣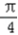 =﹣
=﹣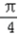 ,即x=0时,f(x)最小为﹣
,即x=0时,f(x)最小为﹣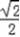 ×
×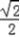 +
+ =0
=0
由﹣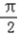 +2kπ≤2x﹣
+2kπ≤2x﹣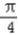 ≤
≤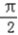 +2kπ,得﹣
+2kπ,得﹣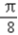 +kπ≤x≤
+kπ≤x≤ +kπ,
+kπ,
由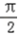 +2kπ≤2x﹣
+2kπ≤2x﹣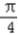 ≤
≤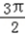 +2kπ,得
+2kπ,得 +kπ≤x≤
+kπ≤x≤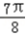 +kπ,
+kπ,
取k=0,结合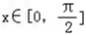
∴函数f(x)的单调增区间为[0, ],单调减区间为[
],单调减区间为[ ,
,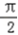 ]
]
(2)∵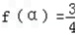 ,∴
,∴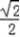 sin(2x﹣
sin(2x﹣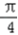 )+
)+ =
=
∴sin(2x﹣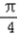 )=
)=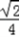
∵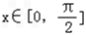 ,∴2x﹣
,∴2x﹣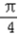 ∈[﹣
∈[﹣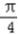 ,
, ]
]
∵0<sin(2x﹣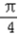 )<
)<
∴2x﹣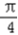 ∈(0,
∈(0,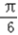 )
)
∴cos(2x﹣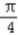 )=
)=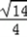
∴sin2x=sin(2x﹣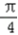 +
+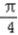 )
)
=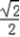 sin(2x﹣
sin(2x﹣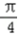 )+
)+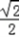 cos(2x﹣
cos(2x﹣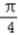 )
)
=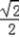 (
(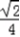 +
+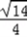 )=
)=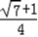
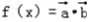 =sin2x+sinxcosx
=sin2x+sinxcosx=
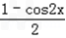 +
+ sin2x=
sin2x= (sin2x﹣cos2x)+
(sin2x﹣cos2x)+
=
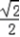 sin(2x﹣
sin(2x﹣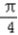 )+
)+ (1)
(1)∵
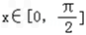 ,∴2x﹣
,∴2x﹣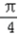 ∈[﹣
∈[﹣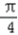 ,
, ]
]∵当2x﹣
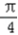 =﹣
=﹣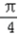 ,即x=0时,f(x)最小为﹣
,即x=0时,f(x)最小为﹣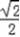 ×
×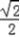 +
+ =0
=0由﹣
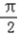 +2kπ≤2x﹣
+2kπ≤2x﹣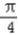 ≤
≤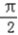 +2kπ,得﹣
+2kπ,得﹣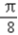 +kπ≤x≤
+kπ≤x≤ +kπ,
+kπ,由
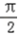 +2kπ≤2x﹣
+2kπ≤2x﹣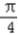 ≤
≤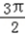 +2kπ,得
+2kπ,得 +kπ≤x≤
+kπ≤x≤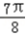 +kπ,
+kπ,取k=0,结合
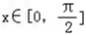
∴函数f(x)的单调增区间为[0,
 ],单调减区间为[
],单调减区间为[ ,
,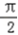 ]
](2)∵
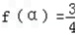 ,∴
,∴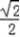 sin(2x﹣
sin(2x﹣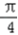 )+
)+ =
=
∴sin(2x﹣
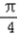 )=
)=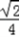
∵
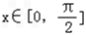 ,∴2x﹣
,∴2x﹣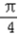 ∈[﹣
∈[﹣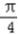 ,
, ]
]∵0<sin(2x﹣
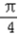 )<
)<
∴2x﹣
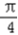 ∈(0,
∈(0,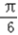 )
)∴cos(2x﹣
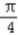 )=
)=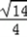
∴sin2x=sin(2x﹣
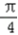 +
+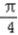 )
)=
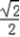 sin(2x﹣
sin(2x﹣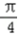 )+
)+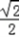 cos(2x﹣
cos(2x﹣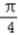 )
)=
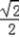 (
(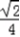 +
+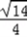 )=
)=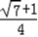

练习册系列答案
相关题目
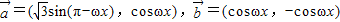 ,函数
,函数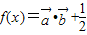 (ω>0)的图象的两相邻对称轴间的距离为
(ω>0)的图象的两相邻对称轴间的距离为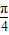 .
.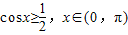 ,且f(x)=m有且仅有一个实根,求实数m的值.
,且f(x)=m有且仅有一个实根,求实数m的值. ,函数
,函数 的最大值为6,最小正周期为π.
的最大值为6,最小正周期为π. 个单位,再向上平移1个单位,得到函数y=g(x)的图象.求
个单位,再向上平移1个单位,得到函数y=g(x)的图象.求 上的值域.
上的值域. ,函数
,函数 的图象一个对称中心与它相邻的一条对称轴之间的距离为1,且其图象过点
的图象一个对称中心与它相邻的一条对称轴之间的距离为1,且其图象过点 .
. ,函数
,函数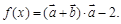 (Ⅰ)求函数
(Ⅰ)求函数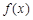 的最小正周期
的最小正周期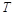 ;(Ⅱ)将函数
;(Ⅱ)将函数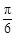 上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数
上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数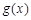 的图像,求函数
的图像,求函数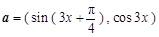 ,函数
,函数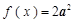 .求:
.求: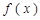 的最小值;
的最小值;