题目内容
已知椭圆 :
: 的右焦点
的右焦点 ,过原点和
,过原点和 轴不重合的直线与椭圆
轴不重合的直线与椭圆 相交于
相交于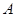 ,
, 两点,且
两点,且 ,
, 最小值为
最小值为 .
.
(Ⅰ)求椭圆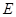 的方程;
的方程;
(Ⅱ)若圆: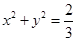 的切线
的切线 与椭圆
与椭圆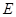 相交于
相交于 ,
, 两点,当
两点,当 ,
, 两点横坐标不相等时,问:
两点横坐标不相等时,问: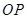 与
与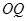 是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
(Ⅰ) 。
。
(Ⅱ) ,
,
解析试题分析:(Ⅰ)设A B(
B( )F(c,0)
)F(c,0) 则
则 1分
1分

 所以有椭圆E的方程为
所以有椭圆E的方程为 5分
5分
(Ⅱ)由题设条件可知直线的斜率存在,设直线L的方程为y=kx+m
L与圆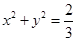 相切,∴
相切,∴ ∴
∴ 7分
7分
L的方程为y=kx+m代入 中得:
中得: 令
令 ,
,  ①
①  ②
②  ③ 10分
③ 10分
∴ 12分
12分
考点:本题主要考查椭圆的标准方程,直线与椭圆的位置关系,平面向量的坐标运算。
点评:难题,求椭圆的标准方程,主要运用了椭圆的几何性质,注意明确焦点轴和a,b,c的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)注意到直线斜率存在,通过联立方程组,应用韦达定理,计算向量的数量积为0,证得垂直关系。

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
 的长轴长为
的长轴长为 ,离心率为
,离心率为 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点 ,且与直线
,且与直线 相切.
相切. 及动圆圆心轨迹
及动圆圆心轨迹 的方程;
的方程; 、
、 ,椭圆
,椭圆 、
、 ,满足
,满足 与
与 共线,
共线, 与
与 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值.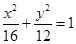 上找一点,使这一点到直线
上找一点,使这一点到直线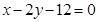 的距离为最小,并求最小值。
的距离为最小,并求最小值。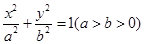 的左、右焦点分别为F1,F2,椭圆的离心率为
的左、右焦点分别为F1,F2,椭圆的离心率为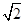 :2.(1)过点C(-1,0)且以向量
:2.(1)过点C(-1,0)且以向量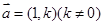 为方向向量的直线
为方向向量的直线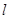 交椭圆于不同两点A、B,若
交椭圆于不同两点A、B,若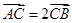 ,则当△OAB的面积最大时,求椭圆的方程。
,则当△OAB的面积最大时,求椭圆的方程。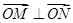 ,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.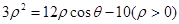
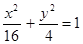 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值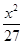 +
+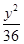 =1有公共的焦点,且与椭圆相交,它们的交点中一个交点的纵坐标是4,求双曲线的标准方程。
=1有公共的焦点,且与椭圆相交,它们的交点中一个交点的纵坐标是4,求双曲线的标准方程。 轴上,且过点
轴上,且过点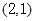 .
.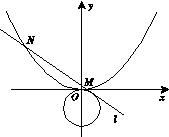
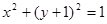 相切的直线
相切的直线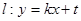 交抛物线于不同的两点
交抛物线于不同的两点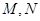 若抛物线上一点
若抛物线上一点 满足
满足
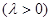 ,求
,求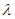 的取值范围.
的取值范围.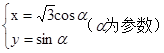 .
.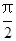 ),判断点P与直线L的位置关系;
),判断点P与直线L的位置关系;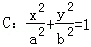 的右焦点F,抛物线:
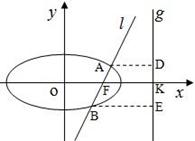
的右焦点F,抛物线: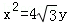 的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且
的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且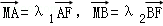 ,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点
,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点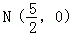 .
.