题目内容
已知抛物线的方程为y2=4x,直线l过定点P(-2,1),斜率为k,k为何值时,直线l与抛物线y2=4x只有一个公共点、有两个公共点、没有公共点?
分析:用解析法解决这个问题,只要讨论直线l的方程与抛物线的方程组成的方程组的解的情况,由方程组解的情况判断直线l与抛物线的位置关系.
解:由题意,设直线l的方程为y-1=k(x+2).
由方程组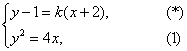 可得ky2-4y+4(2k+1)=0,①
可得ky2-4y+4(2k+1)=0,①
(1)当k=0时,由方程①得y=1,把y=1代入y2=4x,得x=![]() ,这时,直线l与抛物线只有一个公共点(
,这时,直线l与抛物线只有一个公共点(![]() ,1).
,1).
(2)当k≠0时,方程①的判别式为Δ=-16(2k2+k-1).
①由Δ=0,即2k2+k-1=0,解得k=-1或k=![]() ,于是,当k=-1或k=
,于是,当k=-1或k=![]() 时,方程①只有一个解,从而方程组(*)只有一个解.这时,直线l与抛物线只有一个公共点.
时,方程①只有一个解,从而方程组(*)只有一个解.这时,直线l与抛物线只有一个公共点.
②由Δ>0,即2k2+k-1<0,解得-1<k<![]() .于是,当-1<k<
.于是,当-1<k<![]() ,且k≠0时,方程①有两个解,从而方程组(*)有两个解.这时,直线l与抛物线有两个公共点.
,且k≠0时,方程①有两个解,从而方程组(*)有两个解.这时,直线l与抛物线有两个公共点.
③由Δ<0,即2k2+k-1>0,解得k<-1,或k>![]() ,于是当k<-1或k>
,于是当k<-1或k>![]() 时,方程①没有实数解,从而方程组(*)没有解.这时,直线l与抛物线没有公共点.综上,我们可得
时,方程①没有实数解,从而方程组(*)没有解.这时,直线l与抛物线没有公共点.综上,我们可得
当k=-1,或k=![]() ,或k=0时,直线l与抛物线只有一个公共点;
,或k=0时,直线l与抛物线只有一个公共点;
当-1<k<![]() ,且k≠0时,直线l与抛物线有两个公共点;
,且k≠0时,直线l与抛物线有两个公共点;
当k<-1,或k>![]() 时,直线l与抛物线没有公共点.
时,直线l与抛物线没有公共点.
点拨:研究曲线公共点个数,主要是依据方程组解的情况来判定,特别是直线与曲线公共点个数问题,多用判别式来研究,特别要注意的是对二次项系数是否为零要加以讨论.

练习册系列答案
相关题目
已知抛物线的方程为y=2ax2,且过点(1,4),则焦点坐标为( )
| A、(1,0) | ||
B、(
| ||
C、(0,
| ||
| D、(0,1) |
 x2,则它的焦点坐标为( )
x2,则它的焦点坐标为( )