题目内容
16.已知曲线C上任意一点P到两个定点F1(-2$\sqrt{3}$,0)和F2(2$\sqrt{3}$,0)的距离之和为8.(1)求曲线C的方程;
(2)过曲线C内一点M(2,1)引一条弦AB,使弦被点M平分,求这条弦所在直线的方程.
分析 (1)利用椭圆的定义,转化所求曲线方程为椭圆的标准方程,求出椭圆的几何量,即可得到椭圆的方程.
(2)设A(x1,y1)、B(x2,y2),利用平方差法,转化求解AB的斜率,然后求解AB的方程即可.
解答 解:(1)∵$|{P{F_1}}|+|{P{F_2}}|=8>|{{F_1}{F_2}}|=4\sqrt{3}$,
∴曲线C是以F1、F2为焦点,以8为长轴长的椭圆,
∴设$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,
则$\left\{\begin{array}{l}2a=8\\{a^2}-{b^2}={(2\sqrt{3})^2}\end{array}\right.$,
即$\left\{\begin{array}{l}{a^2}=16\\{b^2}=4\end{array}\right.$,
∴曲线C的方程式$\frac{x^2}{16}+\frac{y^2}{4}=1$;
(2)设A(x1,y1)、B(x2,y2),
∵$\frac{{{x_1}^2}}{16}+\frac{{{y_1}^2}}{4}=1$①,$\frac{{{x_2}^2}}{16}+\frac{{{y_2}^2}}{4}=1$②
∴由①-②可得,$\frac{{({x_1}-{x_2})({x_1}+{x_2})}}{16}=-\frac{{({y_1}-{y_2})({y_1}+{y_2})}}{4}$
又∵当lAB⊥x轴时,不符合题意,即(x1-x2)(y1+y2)≠0,
∴${k_{AB}}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=-\frac{4}{16}•\frac{{{x_1}+{x_2}}}{{{y_1}+{y_2}}}=-\frac{1}{4}•\frac{{\frac{{{x_1}+{x_2}}}{2}}}{{\frac{{{y_1}+{y_2}}}{2}}}=-\frac{1}{4}×\frac{2}{1}=-\frac{1}{2}$
∴弦AB所在直线的方程为$y-1=-\frac{1}{2}(x-2)$,
即x+2y-4=0.
点评 本题考查轨迹方程的求法,椭圆的定义的应用,直线与椭圆的位置关系的综合应用,平方差法的应用,考查转化思想以及计算能力.

| 甲 | 82 | 81 | 79 | 78 | 95 | 88 | 93 | 84 |
| 乙 | 92 | 95 | 80 | 75 | 83 | 80 | 90 | 85 |
(2)求两位学生预赛成绩的平均数和方差;
(3)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由.
| A. | $\frac{1}{2}$分米 | B. | 1分米 | C. | 2分米 | D. | 4分米 |
| A. | y轴对称 | B. | x轴对称 | C. | 原点对称 | D. | y=x对称 |
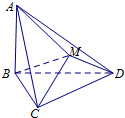 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,