题目内容
若α+β=225°,则(1+tanα)•(1+tanβ)的值为
2
2
.分析:把225°变为180°+45°,利用诱导公式tan(π+α)=tanα及特殊角的三角函数值化简,求出tan225°的值,即为tan(α+β)的值,然后把tan(α+β)利用两角和与差的正切函数公式化简,根据tan(α+β)的值,整理后得到tanα+tanβ=1-tanαtanβ,最后把所求的式子去括号整理后,将tanα+tanβ换为1-tanαtanβ,合并后即可得到值.
解答:解:∵α+β=225°,
∴tan(α+β)=tan225°=tan(180°+45°)
=tan45°=1,
又tan(α+β)=
,
∴
=1,即tanα+tanβ=1-tanαtanβ,
则(1+tanα)•(1+tanβ)
=1+tanα+tanβ+tanαtanβ
=1+1-tanαtanβ+tanαtanβ=2.
故答案为:2
∴tan(α+β)=tan225°=tan(180°+45°)
=tan45°=1,
又tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
∴
| tanα+tanβ |
| 1-tanαtanβ |
则(1+tanα)•(1+tanβ)
=1+tanα+tanβ+tanαtanβ
=1+1-tanαtanβ+tanαtanβ=2.
故答案为:2
点评:此题考查了两角和与差的正切函数公式,诱导公式,以及特殊角的三角函数值,熟练掌握公式,灵活变换角度是解本题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
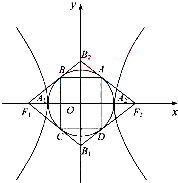 (2012•湖北)如图,双曲线
(2012•湖北)如图,双曲线