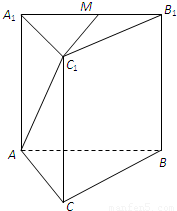
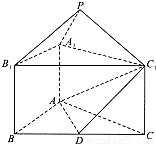
题目内容
如图,正三棱锥ABC-A1B1C1中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=
.
(I)求证:PA1⊥B1C1;
(II)求证:PB1∥平面AC1D;
(III)求多面体PA1B1DAC1的体积.
| 2 |
(I)求证:PA1⊥B1C1;
(II)求证:PB1∥平面AC1D;
(III)求多面体PA1B1DAC1的体积.

证明:(I)取B1C1的中点Q,连A1Q,PQ
∵PB1=PC1,A1B1=A1C1,
∴B1C1⊥A1Q,B1C1⊥PQ
∵A1Q∩PQ=Q
∴B1C1⊥平面A1PQ,∵PA1?平面A1PQ
∴PA1⊥B1C1;
(II)连BQ,在△PB1C1中,PB1=PC1=
,B1C1=2,Q为中点,∴PQ=1
∵BB1=AA1=1
∴BB1=PQ
在平面PBB1CC1中,BB1⊥B1C1,PQ⊥B1C1
∴BB1∥PQ
∴四边形BB1PQ为平行四边形
∴PB1∥BQ
∵BQ∥DC1
∴PB1∥DC1
∴PB1∥平面AC1D;
(III)三棱锥P-A1B1C1的体积为
•
•22• 1 =
多面体ABD-A1B1C1的体积为
•22• 1 -
•
•22• 1• 2=
.
∴多面体PA1B1DAC1的体积为
+
=
.
∵PB1=PC1,A1B1=A1C1,
∴B1C1⊥A1Q,B1C1⊥PQ
∵A1Q∩PQ=Q
∴B1C1⊥平面A1PQ,∵PA1?平面A1PQ
∴PA1⊥B1C1;
(II)连BQ,在△PB1C1中,PB1=PC1=
| 2 |
∵BB1=AA1=1
∴BB1=PQ
在平面PBB1CC1中,BB1⊥B1C1,PQ⊥B1C1
∴BB1∥PQ
∴四边形BB1PQ为平行四边形
∴PB1∥BQ
∵BQ∥DC1
∴PB1∥DC1
∴PB1∥平面AC1D;
(III)三棱锥P-A1B1C1的体积为
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
多面体ABD-A1B1C1的体积为
| ||
| 4 |
| 1 |
| 3 |
| ||
| 8 |
2
| ||
| 3 |
∴多面体PA1B1DAC1的体积为
| ||
| 3 |
2
| ||
| 3 |
| 3 |

练习册系列答案
相关题目
 如图,正三棱锥ABC-A1B1C1的底面边长为a,侧棱长为
如图,正三棱锥ABC-A1B1C1的底面边长为a,侧棱长为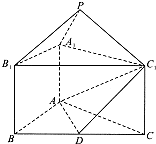 如图,正三棱锥ABC-A1B1C1中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=
如图,正三棱锥ABC-A1B1C1中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=
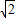 .
.
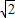 a,M是A1B1的中点.
a,M是A1B1的中点. 是平面ABB1A1的一个法向量;
是平面ABB1A1的一个法向量;