题目内容
已知函数![]() .
.
(Ⅰ)求函数f(x)的最小正周期和图象的对称轴方程;
(Ⅱ)求函数f(x)在区间![]() 上的值域.
上的值域.
考点:
三角函数的周期性及其求法;正弦函数的定义域和值域;正弦函数的对称性.
专题:
综合题.
分析:
(1)先根据两角和与差的正弦和余弦公式将函数f(x)展开再整理,可将函数化简为y=Asin(wx+ρ)的形式,根据T=![]() 可求出最小正周期,令
可求出最小正周期,令![]() ,求出x的值即可得到对称轴方程.(2)先根据x的范围求出2x﹣
,求出x的值即可得到对称轴方程.(2)先根据x的范围求出2x﹣![]() 的范围,再由正弦函数的单调性可求出最小值和最大值,进而得到函数f(x)在区间
的范围,再由正弦函数的单调性可求出最小值和最大值,进而得到函数f(x)在区间![]() 上的值域.
上的值域.
解答:
解:(1)∵![]()
=![]() sin2x+(sinx﹣cosx)(sinx+cosx)
sin2x+(sinx﹣cosx)(sinx+cosx)
=![]() =
=![]()
=![]()
∴周期T=![]()
由![]()
∴函数图象的对称轴方程为![]() (2)∵
(2)∵![]() ,∴
,∴![]() ,
,
因为![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
所以当![]() 时,f(x)取最大值1,
时,f(x)取最大值1,
又∵![]() ,当
,当![]() 时,f(x)取最小值
时,f(x)取最小值![]() ,
,
所以函数f(x)在区间![]() 上的值域为
上的值域为![]() .
.
点评:
本题主要考查两角和与差的正弦公式和余弦公式,以及正弦函数的基本性质﹣﹣最小正周期、对称性、和单调性.考查对基础知识的掌握情况.

练习册系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.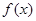 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求