题目内容
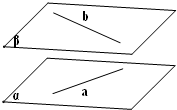（理科）如图，a，b是异面直线，a?α，α∥β，b?β，b∥α，求证：α∥β分析：先过直线b做平面γ根据线面平行的性质定理得到b∥c，进而得到c∥β；再结合a∥β即可证明α∥β．
解答：
证明：如图所示，过直线b做平面γ，
面γ与面α相交于直线c，
则：∵α∩γ=c，β∩γ=b，α∥β
∴b∥c
又∵b?面β，c?面β
∴c∥β
又∵a∥β且a∩c=P
∴α∥β
证明：如图所示，过直线b做平面γ，面γ与面α相交于直线c，
则：∵α∩γ=c，β∩γ=b，α∥β
∴b∥c
又∵b?面β，c?面β
∴c∥β
又∵a∥β且a∩c=P
∴α∥β
点评：本题主要考查面面平行的判定．一般在证明两个平面平行时，在一个平面内找到两条条相交的直线和另一个平面平行．
练习册系列答案
相关题目
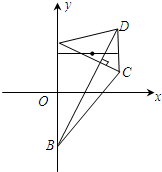
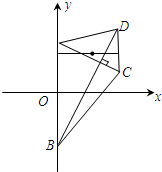（理科）如图，梯形ABCD的底边AB在y轴上，原点O为AB的中点，|AB|=
（理科）如图，在棱长为1的正方体A'C中，过BD及B'C'的中点E作截面BEFD交C'D'于F．
（2008•崇明县一模）（理科）如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PA⊥底面ABCD，PA=4，M为PA的中点，N为BC的中点．