Question

在△ABC中,已知角A为锐角,且

f(A)= 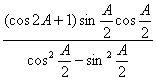+cos²A.

(1)求f(A)的最大值;

(2)若A+B=,f(A)=1,BC=2,求△ABC的三个内角和AC边的长.

Answer 1

解:(1)f(A)=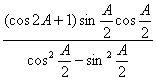+cos²A

=+cos²A=sin2A+cos²A

=(sin2A+cos2A+1)=sin(2A+)+.∵角A为锐角,

∴0＜A＜,＜2A+＜.∴当2A+=时,f(A)取得最大值,其最大值为.

(2)由f(A)=1得sin(2A+)+ =1,∴sin(2A+)=.∴2A+=,A=.

又∵A+B=,∴B=.∴C=.在△ABC中,由正弦定理,得,

∴AC==.