题目内容
函数y=xcosx-sinx,x∈(0,2π)单调增区间是________.
(π,2π)
分析:先求导,进而利用导数与函数的单调性的关系即可得出.
解答:∵函数y=xcosx-sinx,x∈(0,2π),∴y′=-xsinx,
由-xsinx>0,x∈(0,2π),化为sinx>0,x∈(0,2π),解得π<x<2π.
故函数y=xcosx-sinx,x∈(0,2π)单调增区间是(π,2π).
故答案为(π,2π).
点评:熟练掌握利用导数研究函数的单调性的方法是解题的关键.
分析:先求导,进而利用导数与函数的单调性的关系即可得出.
解答:∵函数y=xcosx-sinx,x∈(0,2π),∴y′=-xsinx,
由-xsinx>0,x∈(0,2π),化为sinx>0,x∈(0,2π),解得π<x<2π.
故函数y=xcosx-sinx,x∈(0,2π)单调增区间是(π,2π).
故答案为(π,2π).
点评:熟练掌握利用导数研究函数的单调性的方法是解题的关键.

练习册系列答案
相关题目
函数y=-xcosx的部分图象是( )
A、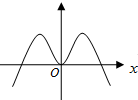 | B、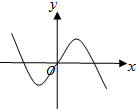 | C、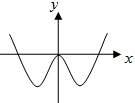 | D、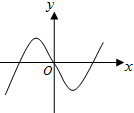 |
函数y=xcosx-sinx在下面哪个区间内是增函数( )
A、(
| ||||
| B、(π,2π) | ||||
C、(
| ||||
| D、(2π,3π) |