题目内容
13.设P(x,y)是圆(x-3)2+y2=4上任一点,则$\frac{y}{x}$的最小值是( )| A. | 0 | B. | -$\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | -1 |
分析 设k=$\frac{y}{x}$,利用圆心(3,0)到直线的距离d=$\frac{|3k|}{\sqrt{{k}^{2}+1}}$≤2即可得到结论.
解答 解:设k=$\frac{y}{x}$,则y=kx,即直线方程为kx-y=0,
∵P(x,y)为圆C上任一点,
∴圆心(3,0)到直线的距离d=$\frac{|3k|}{\sqrt{{k}^{2}+1}}$≤2,
解得-$\frac{2\sqrt{5}}{5}$≤k≤$\frac{2\sqrt{5}}{5}$,
故$\frac{y}{x}$的最小值为$\frac{2\sqrt{5}}{5}$,
故选:B.
点评 本题主要考查直线和圆的位置关系的应用,利用圆心到直线的距离d≤r是解决本题的关键.

练习册系列答案
相关题目
18.直线y=2x-1和圆O2:x2+y2-4y=0的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
3.下列几何体中,轴截面为等腰三角形的是( )
| A. | 圆柱 | B. | 圆锥 | C. | 四棱柱 | D. | 球 |
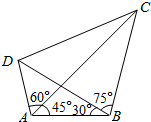 如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.