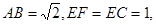题目内容
 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,且AC=AD=CD=DE=2,AB=1.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,且AC=AD=CD=DE=2,AB=1.(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(2)求多面体ABCDE的体积;
(3)求直线EC与平面ABED所成角的正弦值.
分析:(1)因为AB、DE均垂直于底面,可以断定两线段平行,且AB=
DE,可设想取CE、CD的中点,这样可证得BF平行于平面ACD内的直线,从而证得BF平行于平面ACD;
(2)多面体实则是以C为顶点的四棱锥,底面ABED面积易求,可取AD的中点,于C连接后能证明为四棱锥的高,从而可求四棱锥的体积;
(3)连接E与AD的中点,则CE与平面ABED所成的角得到,在直角三角形中直接求其正弦值.
| 1 |
| 2 |
(2)多面体实则是以C为顶点的四棱锥,底面ABED面积易求,可取AD的中点,于C连接后能证明为四棱锥的高,从而可求四棱锥的体积;
(3)连接E与AD的中点,则CE与平面ABED所成的角得到,在直角三角形中直接求其正弦值.
解答: 解:如图,(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,
解:如图,(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则FH∥
ED,且FH=
ED.
∴FH∥=AB,
∴四边形ABFH是平行四边形,∴BF∥AH,
由BF?平面ACD内,AH?平面ACD,∴BF∥平面ACD;
(2)取AD中点G,连接CG,CG⊥AD.
∵AB⊥平面ACD,∴CG⊥AB
又CG⊥AD,AB∩AD=A,∴CG⊥平面ABED,即CG为四棱锥C-ABED的高,
在等边三角形ACD中,CG=
=
.
SABED=
(1+2)×2=3.
∴VC-ABED=
S△AED•
=
×3×
=
.
(3)连接EG,由(2)有CG⊥平面ABED,
∴∠CEG即为直线CE与平面ABED所成的角,设为α,
又在等腰直角三角形CDE中,CE=
DE=2
,
则在Rt△CEG中,有sinα=
=
=
.
 解:如图,(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,
解:如图,(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,设F为线段CE的中点,H是线段CD的中点,
连接FH,则FH∥
| 1 |
| 2 |
| 1 |
| 2 |
∴FH∥=AB,
∴四边形ABFH是平行四边形,∴BF∥AH,
由BF?平面ACD内,AH?平面ACD,∴BF∥平面ACD;
(2)取AD中点G,连接CG,CG⊥AD.
∵AB⊥平面ACD,∴CG⊥AB
又CG⊥AD,AB∩AD=A,∴CG⊥平面ABED,即CG为四棱锥C-ABED的高,
在等边三角形ACD中,CG=
| 22-12 |
| 3 |
SABED=
| 1 |
| 2 |
∴VC-ABED=
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
(3)连接EG,由(2)有CG⊥平面ABED,
∴∠CEG即为直线CE与平面ABED所成的角,设为α,
又在等腰直角三角形CDE中,CE=
| 2 |
| 2 |
则在Rt△CEG中,有sinα=
| CG |
| CE |
| ||
2
|
| ||
| 4 |
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查线面角,考查数形结合与数学转化思想方法,以及空间想象能力、推理论证能力和运算求解能力,属中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
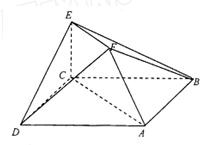 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=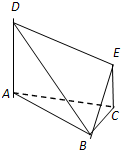 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1. 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=