题目内容
已知a,b∈R+,且满足 的最大值是
的最大值是
- A.

- B.4
- C.

- D.5
C
分析:由a+b=2 得 a2+b2=4-2ab,从而得到S= =4-2ab+2
=4-2ab+2  ,令
,令  =t>0,建立S关于t的二次函数,利用二次函数性质可得S的最大值.
=t>0,建立S关于t的二次函数,利用二次函数性质可得S的最大值.
解答:∵a+b=2,∴a2+b2=4-2ab,∴S= =4-2ab+2
=4-2ab+2  ,
,
令 =t>0,则 S=-2[
=t>0,则 S=-2[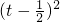 -
- ],
],
故 当t= 时,S有最大值为-2(-
时,S有最大值为-2(- )=
)= ,
,
故选C.
点评:本小题主要考查函数单调性的应用、导一元二次不等式的解法、二次函数的最值等基础知识,考查运算求解能力,考查换元的思想、化归与转化思想.属于基础题.
分析:由a+b=2 得 a2+b2=4-2ab,从而得到S=
 =4-2ab+2
=4-2ab+2  ,令
,令  =t>0,建立S关于t的二次函数,利用二次函数性质可得S的最大值.
=t>0,建立S关于t的二次函数,利用二次函数性质可得S的最大值.解答:∵a+b=2,∴a2+b2=4-2ab,∴S=
 =4-2ab+2
=4-2ab+2  ,
,令
 =t>0,则 S=-2[
=t>0,则 S=-2[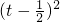 -
- ],
],故 当t=
 时,S有最大值为-2(-
时,S有最大值为-2(- )=
)= ,
,故选C.
点评:本小题主要考查函数单调性的应用、导一元二次不等式的解法、二次函数的最值等基础知识,考查运算求解能力,考查换元的思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
已知a,b∈R,且a>b,则下列不等式中恒成立的是( )
| A、a2>b2 | ||||
B、(
| ||||
| C、lg(a-b)>0 | ||||
D、
|
已知a,b∈R,且a>b,则下列不等式中成立的是( )
A、
| ||||
| B、a2>b2 | ||||
| C、lg(a-b)>0 | ||||
D、(
|
已知a,b∈R,且ab>0,则下列不等式不正确的是( )
| A、|a+b|>a-b | ||||
| B、|a+b|<|a|+|b| | ||||
C、2
| ||||
D、
|