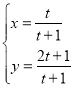Question

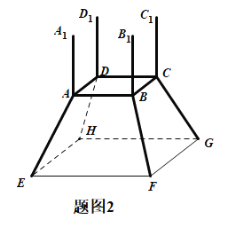
【题目】镇江市长江路江边春江潮广场要设计一尊鼎型塑像（如图1），塑像总高度为12米，塑像由两部分组成，上半部分由四根垂直于水平地面的等高垂直立柱组成（立柱上凸起部分忽略不计），下半部分由正四棱台的上底面四根水平横柱和正四棱台的四根侧棱斜柱组成，如图2所示．设计要求正棱台的水平横柱长度为4米，下底面边长为8米，设斜柱与地面的所成的角为．

（1）用表示塑像上半部分立柱的高度，并求的取值范围？

（2）若该塑像上半部分立柱的造价为千元/米（立柱上凸起部分忽略不计），下半部分横柱和斜柱的造价都为2千元/米，问当为何值时，塑像总造价最低？

Answer 1

【答案】（1）米，的范围为．（2）当时，塑像总造价最低．

【解析】

（1）在平面AEGC内作，利用面面垂直的性质定理可得平面EFGH，为斜柱与地面所成的角，由即可求解.

（2）设总造价为y，则，利用导数即可求解.

解：（1）由正四棱台的定义，平面平面EFGH，

在平面AEGC内作，交EG于M，

平面平面，

则平面EFGH，

则为斜柱与地面所成的角，即．

显然，A，M三点共线，

在等腰梯形AEGC中，，，

则，，立柱，

因为，所以．

答：塑像上半部分的高度米，的范围为．

（2），设总造价为y，

则，

，

记，则，

令，则，所以，

列表：

		0
	减函数	1	增函数

所以当时，有最小值．

答：当时，塑像总造价最低．