题目内容
已知 且
且 ,函数
,函数 ,
, ,记
,记 .
.
(Ⅰ)求函数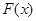 的定义域
的定义域 及其零点;
及其零点;
(Ⅱ)若关于 的方程
的方程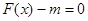 在区间
在区间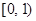 内仅有一解,求实数
内仅有一解,求实数 的取值范围.
的取值范围.
【答案】
(Ⅰ)函数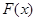 的定义域
的定义域 ,其零点为0;(Ⅱ)①当
,其零点为0;(Ⅱ)①当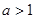 时,实数
时,实数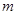 的取值范围为:
的取值范围为: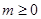 ;②当
;②当 时,实数
时,实数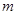 的取值范围为:
的取值范围为: .
.
【解析】
试题分析:(Ⅰ)由已知可得函数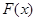 的解析式:
的解析式: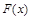
 (
( 且
且 ).由
).由 可得函数
可得函数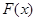 的定义域.令
的定义域.令 ,由对数函数的性质化同底后可解得
,由对数函数的性质化同底后可解得 的值,注意需验证
的值,注意需验证 是否在函数
是否在函数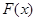 定义域内;(Ⅱ)把关于
定义域内;(Ⅱ)把关于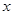 的方程
的方程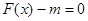 化为:
化为: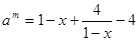 ,设
,设 ,构造函数
,构造函数 ,可得这个函数单调性和最值,从而得
,可得这个函数单调性和最值,从而得 ,最后分
,最后分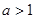 和
和 两种情况可求得实数
两种情况可求得实数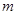 的取值范围.
的取值范围.
试题解析:(1)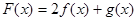
 (
( 且
且 ),由
),由
 ,解得
,解得 ,所以函数
,所以函数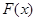 的定义域为
的定义域为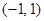 .令
.令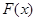
 ,则
,则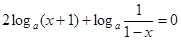 (*)
(*)
方程变为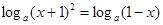 ,
,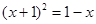 ,即
,即 ,解得
,解得 ,
, 4分
4分
经检验 是(*)的增根,所以方程(*)的解为
是(*)的增根,所以方程(*)的解为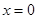 ,所以函数
,所以函数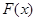 的零点为
的零点为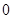 . 6分
. 6分
(2)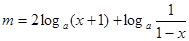 (
( ),
),
 ,
,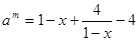 .设
.设 ,则函数
,则函数 在区间
在区间 上是减函数,当
上是减函数,当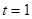 时,此时
时,此时 ,
,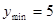 ,所以
,所以 .①若
.①若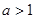 ,则
,则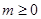 ,方程有解;②若
,方程有解;②若 ,则
,则 ,方程有解.
13分
,方程有解.
13分
考点:1.函数的零点与方程的根的关系;2.函数的定义域和最值.

练习册系列答案
相关题目
 且
且 ,函数
,函数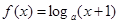 ,
, ,记
,记 .
. 的定义域
的定义域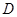 的表达式及其零点;
的表达式及其零点; 的方程
的方程 在区间
在区间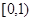 内仅有一解,求实数
内仅有一解,求实数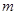 的取值范围.
的取值范围.