题目内容
AB是底部B不可到达的一个建筑物，A为建筑物的最高点，H、G、B三点在同一条水平直线上．在H、G两点用测角仪器测得A的仰角分别是∠ADE=30°、∠ACE=45°、CD=20m，测角仪器的高是h=1m，求建筑物高度AB．
【答案】分析：根据题意可知∠DAC=45°α-30°=15°，求得sin15° 的值，进而利用正弦定理求得AC，进而求得AE，最后根据AB=AE+EB，求得答案．
解答：解：在△ACD中，∠DAC=45°-30°=15°，sin15°=
=
，
由正弦定理可得
，即 
，∴AC=10（
+
）．
Rt△ACE中，AE=AC•sin45°=10（
+1），∴AB=AE+EB=10（
+
）+1 （m），
故建筑物的高度为 10（
+
）+1 （m）．
点评：本题主要考查了解三角形中的实际应用，解题的关键是利用正弦定理，完成了边角问题的互化，属于中档题．
解答：解：在△ACD中，∠DAC=45°-30°=15°，sin15°=
=，由正弦定理可得
，即 ，∴AC=10（+）．Rt△ACE中，AE=AC•sin45°=10（
+1），∴AB=AE+EB=10（+）+1 （m），故建筑物的高度为 10（
+）+1 （m）．点评：本题主要考查了解三角形中的实际应用，解题的关键是利用正弦定理，完成了边角问题的互化，属于中档题．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
AB是底部B不可到达的一个建筑物，A为建筑物的最高点，H、G、B三点在同一条水平直线上．在H、G两点用测角仪器测得A的仰角分别是∠ADE=30°、∠ACE=45°、CD=20m，测角仪器的高是h=1m，求建筑物高度AB．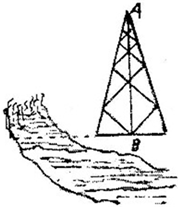
（2012•包头一模）如图，AB是底部B不可到达的一个塔型建筑物，A为塔的最高点．现需在对岸测出塔高AB，甲、乙两同学各提出了一种测量方法，甲同学的方法是：选与塔底B在同一水平面内的一条基线CD，使C，D，B三点不在同一条直线上，测出∠DCB及∠CDB的大小（分别用α，β表示测得的数据）以及C，D间的距离（用s表示测得的数据），另外需在点C测得塔顶A的仰角（用θ表示测量的数据），就可以求得塔离AB．乙同学的方法是：选一条水平基线EF，使E，F，B三点在同一条直线上．在E，F处分别测得塔顶A的仰角（分别用α，β表示测得的数据）以及E，F间的距离（用s表示测得的数据），就可以求得塔高AB．
如图，AB是底部B不可到达的一个塔型建筑物，A为塔的最高点．现需在对岸测出塔高AB，甲、乙两同学各提出了一种测量方法，甲同学的方法是：选与塔底B在同一水平面内的一条基线CD，使C，D，B三点不在同一条直线上，测出∠DCB及∠CDB的大小（分别用α，β表示测得的数据）以及C，D间的距离（用s表示测得的数据），另外需在点C测得塔顶A的仰角（用θ表示测量的数据），就可以求得塔离AB．乙同学的方法是：选一条水平基线EF，使E，F，B三点在同一条直线上．在E，F处分别测得塔顶A的仰角（分别用α，β表示测得的数据）以及E，F间的距离（用s表示测得的数据），就可以求得塔高AB．