题目内容
在长方体ABCD—A1B1C1D1中,∠ABA1=45°,∠CBC1=60°,则∠A1BC1的余弦值是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
思路解析一:如图所示,设长方体的棱长AA1=a,
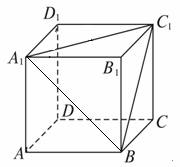
由∠ABA1=45°,则A1B1=B1B=C1C=A1A=a,
A1B=![]() AA1=
AA1=![]() a.
a.
又∠C1BC=60°,
∴B1C1=BC=![]()
BC1=![]()
在Rt△A1B1C1中,A1C1=![]()
在△A1BC1中,由余弦定理,得
cos∠A1BC1=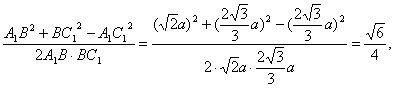
故∠A1BC1的余弦值为![]()
思路解析二:因为平面A1BC1⊥平面C1BB1,
故可证cos∠A1BC1=cos∠A1BB1·cos∠C1BB1.
又∠ABA1=45°,∠C1BC=60°,所以∠A1BB1=90°-∠ABA1=45°.
∠C1BB1=90°-∠C1BC=30°,
从而cos∠A1BC1=cos45°·cos30°=![]() .故选D.
.故选D.
答案:D

练习册系列答案
相关题目
 在长方体ABCD-A'B'C'D'中,AB=
在长方体ABCD-A'B'C'D'中,AB= 如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.