题目内容

若直线l被圆x²+y²=4所截得的弦长为 $数学公式$ ，则直线l与下列曲线一定有公共点的是

A.
y²=x
B.
（x-2）²+y²=4
C.
$数学公式$
D.
$数学公式$

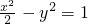
C
分析：根据直线l被圆x²+y²=4所截得的弦长为 $\text{[math]}$ ，可得圆心到直线l的距离为1，从而直线l是圆x²+y²=1的切线，根据圆x²+y²=1在 $\text{[math]}$ 内，即可得到结论．
解答：∵直线l被圆x²+y²=4所截得的弦长为 $\text{[math]}$ ，
∴圆心到直线l的距离为1
∴直线l是圆x²+y²=1的切线
∵圆x²+y²=1在 $\text{[math]}$ 内
∴直线l与 $\text{[math]}$ 一定有公共点
故选C．
点评：本题考查直线与圆相交，考查圆与椭圆的位置关系，确定直线l是圆x²+y²=1的切线是解题的关键．

练习册系列答案

创佳绩课业巧点精练系列答案

单元期末满分大冲刺系列答案

新非凡教辅冲刺100分系列答案

全优课时作业系列答案

英才计划赢在起跑线系列答案

巧思妙算系列答案

全优训练期末测试卷系列答案

新课程成长资源系列答案

新课堂单元测试卷冲刺100分系列答案

学业测评期末考试真题汇编系列答案

相关题目

在平面直角坐标系xOy中，已知直线l：2

=0和圆C₁：x²+y²+8x+F=0．若直线l被圆C₁截得的弦长为2

．
（1）求圆C₁的方程；
（2）设圆C₁和x轴相交于A、B两点，点P为圆C₁上不同于A、B的任意一点，直线PA、PB交y轴于M、N点．当点P变化时，以MN为直径的圆C₂是否经过圆C₁内一定点？请证明你的结论；
（3）若△RST的顶点R在直线x=-1上，S、T在圆C₁上，且直线RS过圆心C₁，∠SRT=30°，求点R的纵坐标的范围．

若直线l被圆C：x²+y²=2所截的弦长不小于2，则l与下列曲线一定有公共点的是（　　）

A、（x-1）²+y²=1

在平面直角坐标系xOy中，已知圆C的方程为x²+y²-8x+15=0，直线l的方程为y=kx-2．
（1）若直线l被圆C所截得弦长为2，求直线l的方程；
（2）若直线l上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，求k的最大值．

已知直线l：y=kx+2（k为常数）过椭圆

=1（（a＞b＞0）的上顶点B和左焦点F，直线l被圆x²+y²=4截得的弦长为d、
（1）若d=2

，求k的值；
（2）若d≥

，求椭圆离心率e的取值范围．

若直线l被圆x²+y²=4所截得的弦长2

，则直线l与下列曲线一定有公共点的是（　　）

C．（x-2）²+y²=4