题目内容
集合A={x|x2-2x-15≤0},B={x|a+1≤x≤4a+1},B⊆A,则a的取值范围是________.
(-4,1]
分析:解出集合A中的不等式,可得集合A={x|x2-2x-15≤0}=[-3,5],再由B={x|a+1≤x≤4a+1},B⊆A,建立关于a的不等式组,解之即得实数a的取值范围.
解答:对于集合A={x|x2-2x-15≤0},
不等式x2-2x-15≤0的解集为:[-3,5]
∵B={x|a+1≤x≤4a+1},B⊆A,
∴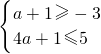 ?-4≤a≤1
?-4≤a≤1
故答案为:(-4,1]
点评:本题考查了集合关系中的参数取值问题,属于基础题.处理该问题时可以结合数轴加以理解,解题时要注意区间端点的取值问题.
分析:解出集合A中的不等式,可得集合A={x|x2-2x-15≤0}=[-3,5],再由B={x|a+1≤x≤4a+1},B⊆A,建立关于a的不等式组,解之即得实数a的取值范围.
解答:对于集合A={x|x2-2x-15≤0},
不等式x2-2x-15≤0的解集为:[-3,5]
∵B={x|a+1≤x≤4a+1},B⊆A,
∴
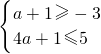 ?-4≤a≤1
?-4≤a≤1故答案为:(-4,1]
点评:本题考查了集合关系中的参数取值问题,属于基础题.处理该问题时可以结合数轴加以理解,解题时要注意区间端点的取值问题.

练习册系列答案
相关题目