题目内容
设ω=cos +isin
+isin ,则以ω,ω3,ω7,ω9为根的方程是
,则以ω,ω3,ω7,ω9为根的方程是
- A.x4+x3+x2+x+1=0
- B.x4-x3+x2-x+1=0
- C.x4-x3-x2+x+1=0
- D.x4+x3+x2-x-1=0
B
分析:根据题目给出的ω,可求得其5次方为1,所以ω=cos +isin
+isin 是x5+1=0的一个虚根,而方程x5+1=(x+1)(x4-x3+x2-x+1)=0的另外四个根就是ω,ω3,ω7,ω9
是x5+1=0的一个虚根,而方程x5+1=(x+1)(x4-x3+x2-x+1)=0的另外四个根就是ω,ω3,ω7,ω9
解答:因为ω=cos +isin
+isin ,所以ω5+1=
,所以ω5+1= +1=cosπ+isinπ+1=0,
+1=cosπ+isinπ+1=0,
所以ω=cos +isin
+isin 是方程x5+1=0的一个根,
是方程x5+1=0的一个根,
因为-1=cosπ+isinπ,
则-1的5次方根为 (k=0,1,2,3,4),
(k=0,1,2,3,4),
当k=0时为ω,当k=1时为ω3,当k=3时为ω7,当k=4时为ω9,
而x5+1=(x+1)(x4-x3+x2-x+1)=0,
故ω,ω3,ω7,ω9 都是方程x4-x3+x2-x+1=0.
故选B.
点评:本题考查复数三角形式的混合运算,注意ω=cos +isin
+isin 是x5+1=0的一个虚根,是基础题.
是x5+1=0的一个虚根,是基础题.
分析:根据题目给出的ω,可求得其5次方为1,所以ω=cos
 +isin
+isin 是x5+1=0的一个虚根,而方程x5+1=(x+1)(x4-x3+x2-x+1)=0的另外四个根就是ω,ω3,ω7,ω9
是x5+1=0的一个虚根,而方程x5+1=(x+1)(x4-x3+x2-x+1)=0的另外四个根就是ω,ω3,ω7,ω9解答:因为ω=cos
 +isin
+isin ,所以ω5+1=
,所以ω5+1= +1=cosπ+isinπ+1=0,
+1=cosπ+isinπ+1=0,所以ω=cos
 +isin
+isin 是方程x5+1=0的一个根,
是方程x5+1=0的一个根,因为-1=cosπ+isinπ,
则-1的5次方根为
 (k=0,1,2,3,4),
(k=0,1,2,3,4),当k=0时为ω,当k=1时为ω3,当k=3时为ω7,当k=4时为ω9,
而x5+1=(x+1)(x4-x3+x2-x+1)=0,
故ω,ω3,ω7,ω9 都是方程x4-x3+x2-x+1=0.
故选B.
点评:本题考查复数三角形式的混合运算,注意ω=cos
 +isin
+isin 是x5+1=0的一个虚根,是基础题.
是x5+1=0的一个虚根,是基础题. 
练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
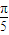 +isin
+isin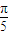 ,则以ω,ω3,ω7,ω9为根的方程是( )
,则以ω,ω3,ω7,ω9为根的方程是( )