题目内容
【题目】已知函数![]() ,且
,且![]() 在
在![]() 和
和![]() 处取得极值.
处取得极值.
(1)求函数![]() 的解析式;
的解析式;
(2)设函数![]() ,是否存在实数
,是否存在实数![]() ,使得曲线
,使得曲线![]() 与
与![]() 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)由f(x)=ax3+bx2-2x在x=1或2处取得极值,可得f'(1)=f'(2)=0,故可得到a、b的方程组,求解即可;
(2)曲线y=g(x)与x轴有两个交点,转化成g(x)=0有两个不同的实数解,然后利用导数研究函数的单调性和极值,然后依题意有g(x)极大值=0或g(x)极小值=0即可求出t的值.
试题解析:(1)![]() ,
,
因为![]() 在
在![]() 和
和![]() 处取得极值,
处取得极值,
所以![]() 和
和![]() 是
是![]() 的两个根,
的两个根,
则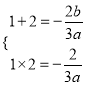 ,解得
,解得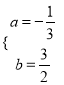 ,
,
经检验符合已知条件,故![]() ;
;
(2)由题意知![]() ,
,
令![]() 得,
得, ![]() 或
或![]() ,
,
![]() 随着
随着![]() 变化情况如下表所示:
变化情况如下表所示:
|
| 1 |
| 2 |
|
| - | 0 | + | 0 | - |
| 递减 | 极小值 | 递增 | 极大值 | 递减 |
由上表可知![]() ,
,
又![]() 取足够大的正数时,
取足够大的正数时, ![]() ,
,
![]() 取足够小的负数时,
取足够小的负数时, ![]() ,
,
因此,为使曲线![]() 与
与![]() 轴有两个交点,结合
轴有两个交点,结合![]() 的单调性,
的单调性,
得![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
即存在![]() ,且
,且![]() 或
或![]() 时,曲线
时,曲线![]() 与
与![]() 轴有两个交点.
轴有两个交点.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
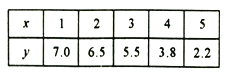
【题目】调查某校 100 名学生的数学成绩情况,得下表:
一般 | 良好 | 优秀 | |
男生(人) |
| 18 |
|
女生(人) | 10 | 17 |
|
已知从这批学生中随机抽取1名学生,抽到成绩一般的男生的概率为0.15.
(1)求![]() 的值;
的值;
(2)若用分层抽样的方法,从这批学生中随机抽取20名,问应在优秀学生中抽多少名?
(3)已知![]() ,优秀学生中男生不少于女生的概率.
,优秀学生中男生不少于女生的概率.