题目内容

已知圆的方程x2+y2-2x-4y=0，设圆过点（1，3）的最长弦和最短弦分别为AB和CD，则四边形ABCD的面积为（　　）
分析：由圆的知识可知过（1，3）的最长弦为直径，最短弦为过（1，3）且垂直于该直径的弦，然后利用对角线垂直的四边形的面积等于对角线乘积的一半求出即可．
解答：解：圆的标准方程为（x-1）2+（y-2）2=5，
由题意得最长的弦|AC|=2
5
，圆心（1，2），圆心与点（1，3）的距离d=1
根据勾股定理得最短的弦|BD|=2
(
5
)2-12
=4，且AC⊥BD，
四边形ABCD的面积S=
1
2
|AC|×|BD|=
1
2
×2
5
×4=4
5

故选B
点评：本题考查学生灵活运用几何知识决数学问题的能力，掌握对角线垂直的四边形的面积计算方法为对角线乘积的一半是解决问题的关键，属基础题．
练习册系列答案
相关题目
已知圆的方程x2+y2=25，过M（-4，3）作直线MA，MB与圆交于点A，B，且MA，MB关于直线y=3对称，则直线AB的斜率等于（　　）
A、-
4
3
B、-
3
4
C、-
5
4
D、-
4
5
已知圆的方程x2+y2=25，过M（-4，3）作直线MA，MB与圆交于点A，B，且MA，MB关于直线y=3对称，则直线AB的斜率等于
 
．
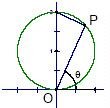精英家教网已知圆的方程x2+（y-1）2=1，P为圆上任意一点（不包括原点）．直线OP的倾斜角为θ弧度，|OP|=d，则d=f（θ）的图象大致为
 
已知圆的方程x2+y2=4，若抛物线过点A（0，-1），B（0，1）且以圆的切线为准线，则抛物线的焦点轨迹方程是（　　）
A、
x2
3
+
y2
4
=1（y≠0）
B、
x2
4
+
y2
3
=1（y≠0）
C、
x2
3
+
y2
4
=1（x≠0）
D、
x2
4
+
y2
3
=1（x≠0）
已知圆的方程x2+y2=4，若抛物线过定点A（0，1），B（0，-1）且以圆的切线为准线，则抛物线焦点的轨迹方程是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网