题目内容
有一种大型商品,A、B两地都有出售,且价格相同,某地居民从两地之一购得商品后运回的费用是:A地每公里的运费是B地每公里运费的3倍.已知A、B两地距离为10公里,顾客选择A地或B地购买这件商品的标准是:包括运费和价格的总费用较低.求P地居民选择A地或B地购物总费用相等时,点P所在曲线的形状,并指出曲线上、曲线内、曲线外的居民应如何选择购物地点?
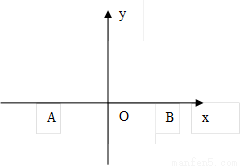
分析:以A、B所在的直线为x轴,线段AB的中点为原点建立直角坐标系,求出由P地到A、B两地购物总费用,可求P地居民选择A地或B地购物总费用相等时,点P所在曲线的形状,进而根据P的位置,即可得出结论.
解答:解:如图,以A、B所在的直线为x轴,线段AB的中点为原点建立直角坐标系,
∵|AB|=10,∴A(-5,0),B(5,0).
设P(x,y),P到A、B两地购物的运费分别是3a、a(元/公里).
当由P地到A、B两地购物总费用相等时,有:价格+A地运费=价格+B地运费,
得3a
=a
,化简整理得(x+
)2+y2=(
)2,
(1)当P点在以(-
,0)为圆心、
为半径的圆上时,居民到A地或B地购物总费用相等.
(2)当P点在上述圆内时,
,
∴[9(x+5)2+9y2]-[(x-5)2+y2]=8[(x+
)2+y2-(
)2]<0.
∴3a
<a
,故此时到A地购物合算.
(3)同理,当P点在上述圆外时,得3a
>a
,故此时到B地购物合算.

∵|AB|=10,∴A(-5,0),B(5,0).
设P(x,y),P到A、B两地购物的运费分别是3a、a(元/公里).
当由P地到A、B两地购物总费用相等时,有:价格+A地运费=价格+B地运费,
得3a
| (x+5)2+y2 |
| (x-5)2+y2 |
| 25 |
| 4 |
| 15 |
| 4 |
(1)当P点在以(-
| 25 |
| 4 |
| 15 |
| 4 |
(2)当P点在上述圆内时,
|
∴[9(x+5)2+9y2]-[(x-5)2+y2]=8[(x+
| 25 |
| 4 |
| 15 |
| 4 |
∴3a
| (x+5)2+y2 |
| (x-5)2+y2 |
(3)同理,当P点在上述圆外时,得3a
| (x+5)2+y2 |
| (x-5)2+y2 |
点评:本题考查轨迹方程,考查学生利用数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
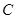 的形状;
的形状;