题目内容
8.一个几何体的三视图如图所示,则这个几何体的体积为( )
| A. | $\frac{(9+2π)\sqrt{3}}{6}$ | B. | $\frac{(8+2π)\sqrt{3}}{6}$ | C. | $\frac{(6+π)\sqrt{3}}{6}$ | D. | $\frac{(8+π)\sqrt{3}}{6}$ |
分析 这个几何体由半个圆锥与一个四棱锥组合而成,从而求两个体积之和即可.
解答 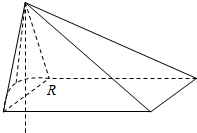 解:这个几何体由半个圆锥与一个四棱锥组合而成,
解:这个几何体由半个圆锥与一个四棱锥组合而成,
半个圆锥的体积为$\frac{1}{3}$×$\frac{1}{2}$×π×1×$\sqrt{3}$=$\frac{1}{6}$$π\sqrt{3}$;
四棱锥的体积为$\frac{1}{3}$×2×2×$\sqrt{3}$=$\frac{4}{3}$$\sqrt{3}$;
故这个几何体的体积V=$\frac{(8+π)\sqrt{3}}{6}$;
故选D.
点评 本题考查了学生的空间想象力与计算能力,属于基础题.

练习册系列答案
相关题目
20.在边长为1的正三角形ABC中任取一点M,则AM<$\frac{\sqrt{3}}{2}$的概率为( )
| A. | $\frac{\sqrt{3}π}{18}$ | B. | $\frac{\sqrt{3}π}{12}$ | C. | $\frac{\sqrt{3}π}{9}$ | D. | $\frac{\sqrt{3}π}{6}$ |
17.已知集合A={x|1<x<4},B={x|x≤2},则A∩(∁RB)等于( )
| A. | (1,2] | B. | [2,4) | C. | (2,4) | D. | (1,4) |
18.设集合M={x|x2-2x-3<0,x∈Z},则集合M的真子集个数为( )
| A. | 8 | B. | 7 | C. | 4 | D. | 3 |

 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.