题目内容
如图所示,AO⊥平面α,BC⊥OB,BC与平面α夹角为30°,AO=BO=BC=a,求AC的长.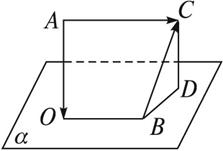
解：作CD⊥平面α,则∠DBC=30°.
所以∠BCD=60°,
所以〈
〉=120°,即〈
,
〉=120°.
又因为
所以｜
｜2=3a2+2·a2·cos120°=2a2.
所以｜
｜=
a,即AC=
a.
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
如图所示,AO⊥平面α,BC⊥OB,BC与平面α夹角为30°,AO=BO=BC=a,求AC的长.
解：作CD⊥平面α,则∠DBC=30°.
所以∠BCD=60°,
所以〈〉=120°,即〈,〉=120°.
又因为
所以｜｜2=3a2+2·a2·cos120°=2a2.
所以｜｜=a,即AC=a.
名校课堂系列答案
在平面直角坐标系xOy中，抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO（如图所示）．则△AOB得重心G（即三角形三条中线的交点）的轨迹方程为
如图所示，AO⊥平面α，BC⊥OB，BC与平面α的夹角为30°，AO=BO=BC=a，则AC=
如图所示，已知△AOB中，
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得，已知FA⊥