题目内容
已知y与x(x≤100)之间的部分对应关系如下表:
| x | 11 | 12 | 13 | 14 | 15 | … |
| y | 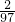 |  |  |  |  | … |
y(108-x)=2
分析:首先x的值依次成等差数列,然后将y值的分子统一化成2,这样分母依次是97、96、95、94、93,可见y的分母成等差数列,对照它们的通项公式可得y(108-x)=2.
解答:首先看x:11,12,13,14,15成首项为11公差等于1的等差数列,
由等差数列通项公式得xn=10+n…(1)
再将y值的分子统一化成2,写成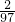 ,
, ,
, ,
, ,
, 的形式,
的形式,
分母成等差数列,可知分母an=98-n
因此 …(2)
…(2)
(1)、(2)两式消去n,得yn(108-xn)=2
故答案为:y(108-x)=2
点评:本题考查了等差数列的通项公式以及函数解析式求解常用方法,属于中档题.
分析:首先x的值依次成等差数列,然后将y值的分子统一化成2,这样分母依次是97、96、95、94、93,可见y的分母成等差数列,对照它们的通项公式可得y(108-x)=2.
解答:首先看x:11,12,13,14,15成首项为11公差等于1的等差数列,
由等差数列通项公式得xn=10+n…(1)
再将y值的分子统一化成2,写成
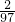 ,
, ,
, ,
, ,
, 的形式,
的形式,分母成等差数列,可知分母an=98-n
因此
 …(2)
…(2)(1)、(2)两式消去n,得yn(108-xn)=2
故答案为:y(108-x)=2
点评:本题考查了等差数列的通项公式以及函数解析式求解常用方法,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
