题目内容
从{1,2,3}中随机选取一个数a,从{1,2,3,4,5,6}中随机选取一个数b,则使log2ab=1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由题意知本题是一个古典概型,试验包含的所有事件根据分步计数原理知共有3×6种结果,而满足条件的事件是a=1,b=2;a=2,b=4;a=3,b=6共有3种结果.
解答:解:由题意知本题是一个古典概型,
∵从{1,2,3}中随机选取一个数a,从{1,2,3,4,5,6}中随机选取一个数b,
∴根据分步计数原理知试验包含的所有事件共有3×6=18种结果,
由于log2ab=1,则b=2a,
故满足条件的事件是a=1,b=2; a=2,b=4; a=3,b=6,共有3种结果,
∴由古典概型公式得到P=
=
,
故选:C.
∵从{1,2,3}中随机选取一个数a,从{1,2,3,4,5,6}中随机选取一个数b,
∴根据分步计数原理知试验包含的所有事件共有3×6=18种结果,
由于log2ab=1,则b=2a,
故满足条件的事件是a=1,b=2; a=2,b=4; a=3,b=6,共有3种结果,
∴由古典概型公式得到P=
| 3 |
| 18 |
| 1 |
| 6 |
故选:C.
点评:本题考查古典概型及其概率计算公式的应用,属于基础题.

练习册系列答案
相关题目
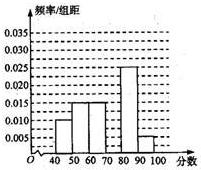 某校参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩分成六段[40,50)、[50,60)、…、[90,100]后得到如图部分频率分布直方图,观察图形的信息,回答下列问题:
某校参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩分成六段[40,50)、[50,60)、…、[90,100]后得到如图部分频率分布直方图,观察图形的信息,回答下列问题:




