Question

已知椭圆C的方程为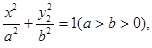左、右焦点分别为F₁、F₂，焦距为4，点M是椭圆C上一点，满足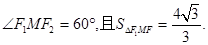

（Ⅰ）求椭圆C的方程；

（Ⅱ）过点P（0，2）分别作直线PA，PB交椭圆C于A，B两点，设直线PA，PB的斜率分别为k₁，k₂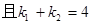，，求证：直线AB过定点，并求出直线AB的斜率k的取值范围。

 

Answer 1

【答案】

（Ⅰ）（Ⅱ）或.

【解析】

试题分析：（Ⅰ）在 中,设,,由余弦定理得，

即，即，得.

又因为，，，

又因为所以，

所以所求椭圆的方程为.                    

（Ⅱ）显然直线的斜率存在，设直线方程为，，

由得，即，

，，

由得，，又，，

则，，

，

那么，

则直线过定点.                

因为，，

，

，，

，所以或.  

考点：直线与圆锥曲线的综合问题；椭圆的标准方程．

点评：本题主要考查了直线与圆锥曲线的综合问题．此类题综合性强，要求学生要有较高地转化数学思想的运用能力，能将已知条件转化到基本知识的运用