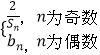题目内容
【题目】交强险是车主必须为机动车购买的险种，若普通6座以下私家车投保交强险第一年的费用 (基准保费)统一为
元，在下一年续保时，实行的是费率浮动机制，保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费
基准保费
（
浮动比率
).发生交通事故的次数越多，出险次数的就越多，费率也就越髙，具体浮动情况如下表：
某机构为了研究某一品牌普通6座以下私家车的投保情况，为此搜集并整理了100辆这一品牌普通6座以下私家车一年内的出险次数，得到下面的柱状图：
已知小明家里有一辆该品牌普通6座以下私家车且需要续保，续保费用为
元.
（1）记
为事件“
”，求
的估计值；
（2）求
的平均估计值.
【答案】（1）0.55.（2）1.14a.
【解析】试题分析：（1）由所给数据知，事件
发生当且仅当一年内出险次数大于或等于1且小于或等于4，由此可求
的估计值；
（2）由期望的计算公式可得.
试题解析：（（1）由所给数据知，事件
发生当且仅当一年内出险次数大于或等于1且小于或等于4，
所以
.
（2）由题可知
的平均估计值为
.
【题目】已知二次函数
的最小值为3，且
.
求函数
的解析式；
（2）若偶函数
（其中
），那么， 
在区间
上是否存在零点？请说明理由.
【答案】（1）
（2）存在零点
【解析】试题分析：（1）待定系数法，己知函数类型为二次函数，又知f(-1)=f(3),所以对称轴是x=1,且函数最小值f(1)=3,所设函数
，且
，代入f(-1)=11，可解a。
（2）由题意可得
，代入
，由
和根的存在性定理， 
在区间（1，2）上存在零点。
试题解析：（1）因为
是二次函数，且
所以二次函数图像的对称轴为
．
又
的最小值为3，所以可设
，且
由
，得
所以
（2）由（1）可得
，
因为
，
所以
在区间（1，2）上存在零点．
【点睛】
（1）对于求己知类型函数的的解析式，常用待定系数法，由于二次函数的表达式形式比较多，有一般式，两点式，顶点式，由本题所给条件知道对称轴与顶点坐标，所以设顶点式。
（2）对于判定函数在否存在零点问题，一般解决此类问题的三步曲是：①先通过观察函数图象再估算出根所在的区间；②根据方程根的存在性定理证明根是存在的；③最后根据函数的性质证明根是唯一的.本题给了区间，可直接用根的存在性定理。
【题型】解答题
【结束】
20
【题目】《中华人民共和国个人所得税》规定，公民月工资、薪金所得不超过3500元的部分不纳税，超过3500元的部分为全月税所得额，此项税款按下表分段累计计算：
全月应纳税所得额 | 税率 |
不超过1500元的部分 |
|
超过1500元至4500元的部分 |
|
超过4500元至9000元的部分 |
|
（1）已知张先生的月工资，薪金所得为10000元，问他当月应缴纳多少个人所得税？
（2）设王先生的月工资，薪金所得为
，当月应缴纳个人所得税为
元，写出
与
的函数关系式；
（3）已知王先生一月份应缴纳个人所得税为303元，那么他当月的工资、薪金所得为多少？
