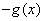题目内容
观察 ,
, ,则归纳推理可得:若定义在R上的函数
,则归纳推理可得:若定义在R上的函数 满足
满足 ,记
,记 为
为 的导函数,则
的导函数,则 =
=
A.  B.
B.
 C.
C.
 D.
D.

【答案】
C
【解析】解:由给出的例子可以归纳推理得出:
若函数f(x)是偶函数,则它的导函数是奇函数,
因为定义在R上的函数f(x)满足f(-x)=f(x),
即函数f(x)是偶函数,
所以它的导函数是奇函数,即有g(-x)=-g(x),
故选C.

练习册系列答案
相关题目
观察 ,
, ,
,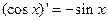 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在 上的函数
上的函数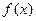 满足
满足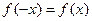 ,记
,记 的导函数,则
的导函数,则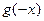
A.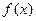 | B.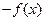 | C.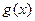 | D.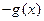 |
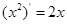 ,
,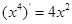 ,
,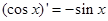 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在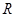 上的函数
上的函数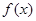 满足
满足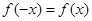 ,记
,记 的导函数,则
的导函数,则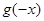
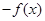 (C)
(C)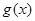 (D)
(D)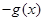
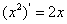 ,
,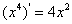 ,
,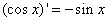 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在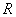 上的函数
上的函数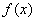 满足
满足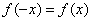 ,记
,记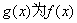 的导函数,则
的导函数,则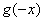
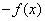 (C)
(C) (D)
(D)