题目内容
19.定义在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{3}}(x+1),x∈[0,2)}\\{-\frac{1}{2}{x}^{2}+4x-7,x∈[2,+∞)}\end{array}\right.$,则关于x的方程f(x)=a(0<a<1)的所有根之和为( )| A. | 3-a-1 | B. | 1-3-a | C. | 3a-1 | D. | 1-3a |
分析 利用奇函数得出当x≥0时,f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{3}}(x+1),x∈[0,2)}\\{-\frac{1}{2}{x}^{2}+4x-7,x∈[2,+∞)}\end{array}\right.$,画出图象,根据对称性得出零点的值满足x1+x2,x4+x5的值,关键运用对数求解x3=1-3a,整体求解即可.
解答  解:∵定义在R上的奇函数f(x),
解:∵定义在R上的奇函数f(x),
∴f(-x)=-f(x),
∵当x≥0时,f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{3}}(x+1),x∈[0,2)}\\{-\frac{1}{2}{x}^{2}+4x-7,x∈[2,+∞)}\end{array}\right.$,
得出x<0时,f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(1-x),x∈(-2,0)}\\{\frac{1}{2}{x}^{2}+4x+7,x∈(-∞,-2]}\end{array}\right.$.
画出图象得出:
如图从左向右零点为x1,x2,x3,x4,x5,
根据对称性得出:x1+x2=-4×2=-8,
x4+x5=2×4=8,-$lo{g}_{\frac{1}{3}}$(-x3+1)=a,
x3=1-3a,
故x1+x2+x3+x4+x5=-8+1-3a+8=1-3a,
故选:D.
点评 本题综合考查函数的性质,图象的运用,函数的零点与函数交点问题,考查了数形结合的能力,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
14.某商场2014年一月份到十二月份销售额呈现先下降后上升的趋势,下列函数模型中能较准确反映该商场月销售额f(x)与月份x关系的是( )
| A. | f(x)=a•bn(b>0,且b≠1) | B. | f(x)=lognx+b(a>0,且a≠1) | ||
| C. | f(x)=x2+ax+b | D. | f(x)=$\frac{a}{x}+b$ |
4.已知等比数列{an}的各项均为正数,公比q≠1,记P=$\frac{{a}_{2}+{a}_{10}}{2}$,Q=$\sqrt{{a}_{5}{a}_{7}}$,则P与Q的大小关系是( )
| A. | P<Q | B. | P>Q | C. | P=Q | D. | 无法确定 |
8.点的集合M={(x,y)|xy>0}是指( )
| A. | 第一象限内点的集合 | B. | 第三象限内点的集合 | ||
| C. | 第一、三象限内点的集合 | D. | 第二、四象限内点的集合 |
9.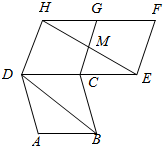 如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )
如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )
 如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )
如图,四边形ABCD,CEFG,CGFD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是( )| A. | |$\overrightarrow{AB}$|=|$\overrightarrow{EF}$| | B. | $\overrightarrow{AB}$与$\overrightarrow{FH}$共线 | C. | $\overrightarrow{BD}$与$\overrightarrow{EH}$共线 | D. | $\overrightarrow{DC}$与$\overrightarrow{EC}$共线 |