题目内容
设ω＞0，若函数f（x）=2sinωx在[-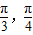
，]上单调递增，则ω的取值范围是 ．
【答案】分析：由三角函数的图象：知在[-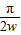
，0]上是单调增函数，结合题意得
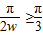，从而求出ω的取值范围．
解答：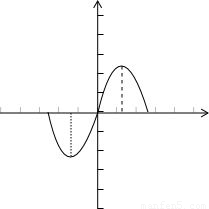
解：由三角函数f（x）=2sinωx的图象：
知在[-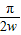
，0]上是单调增函数，
结合题意得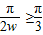
，
从而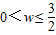
，即为ω的取值范围．
故填：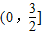
．
点评：本题主要考查三角函数的单调性，本题巧妙地运用了正弦函数的单调性，给出了简捷的计算，解题时应注意把数形结合思想的灵活应用．
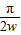，0]上是单调增函数，结合题意得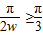，从而求出ω的取值范围．解答：
解：由三角函数f（x）=2sinωx的图象：知在[-
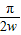，0]上是单调增函数，结合题意得
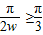，从而
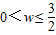，即为ω的取值范围．故填：
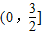．点评：本题主要考查三角函数的单调性，本题巧妙地运用了正弦函数的单调性，给出了简捷的计算，解题时应注意把数形结合思想的灵活应用．
练习册系列答案
相关题目