题目内容
数列 的前
的前 项组成集合
项组成集合 ,从集合
,从集合 中任取
中任取 个数,其所有可能的
个数,其所有可能的 个数的乘积的和为
个数的乘积的和为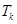 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记 .例如:当
.例如:当 时,
时, ,
, ,
,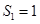 ;当
;当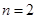 时,
时, ,
, ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)猜想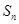 ,并用数学归纳法证明.
,并用数学归纳法证明.
(Ⅰ)63; (Ⅱ) .
.
解析试题分析:(Ⅰ)通过列举进行计算;(Ⅱ)先从特殊入手,
当 时,
时, ,
, ,
, ;
;
当 时,
时, ,
, ,
, ,所以
,所以 ;
;
从特殊到一般探求 与
与 之间的递推关系,从而便于用数学归纳法证明.
之间的递推关系,从而便于用数学归纳法证明.
试题解析:(Ⅰ)当 时,
时, ,
, ,
, ,所以
,所以 ;
;
(Ⅱ)由 ,
, ,
,
猜想 ,下面证明:
,下面证明:
(1)易知 时成立;
时成立;
(2)假设 时
时 ,
,
则 时,
时,

(其中 ,为
,为 时可能的
时可能的 个数的乘积的和为
个数的乘积的和为 ),
),




即 时
时 也成立,
也成立,
综合(1)(2)知对 ,
, 成立.
成立.
所以 .
.
考点:归纳推理、数学归纳法.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
设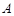 是由
是由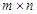 个实数组成的
个实数组成的 行
行 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(Ⅰ) 数表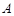 如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
表1
| 1 | 2 | 3 |  |
 | 1 | 0 | 1 |
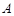 如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数 的所有可能值;
的所有可能值;表2

(Ⅲ)对由
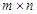 个实数组成的
个实数组成的 行
行 列的任意一个数表
列的任意一个数表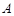 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由. 若x+yi=1+2xi(x,y∈R),则x﹣y等于( )
| A.0 | B.﹣1 | C.1 | D.2 |
下面是关于复数z= 的四个命题
的四个命题
P1: =2 p2:
=2 p2: =2i P3:z的共轭复数为1+i P4:z的虚部为-1
=2i P3:z的共轭复数为1+i P4:z的虚部为-1
其中真命题为( )
| A.P2 ,P3 | B.P1 ,P2 | C.P2,P4 | D.P3 , P4 |
 是一个自然数,
是一个自然数, 是
是 :
: 是自然数,
是自然数, (
( ,
, ).
). ,
, ;
; ,求证:
,求证: ;
; 时,求证:存在
时,求证:存在 ,使得
,使得 .
. 对于一切n∈N*都成立?若存在,求出a,b的值,若不存在,请说明理由。
对于一切n∈N*都成立?若存在,求出a,b的值,若不存在,请说明理由。
 +
+ ≥
≥ .
.