题目内容
已知函数f(x)=| 4x |
| 3x2+3 |
(1)求f(x)的值域;
(2)设a≠0,函数g(x)=
| 1 |
| 3 |
分析:(1)求出f(x)的导函数,令导函数等于求出x的值,然后由x的值,分区间讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值即可得到f(x)的值域;
(2)设函数g(x)在[0,2]上的值域是A,根据题意对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0,得到区间[0,2]是A的子集,求出g(x)的导函数,分a小于0和a大于0两种情况讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值,即可得到函数在相应区间的值域,根据区间[0,2]是A的子集判断出符合这一条件的情况,列出关于a的不等式,求出不等式的解集即可得到满足题意a的取值范围.
(2)设函数g(x)在[0,2]上的值域是A,根据题意对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0,得到区间[0,2]是A的子集,求出g(x)的导函数,分a小于0和a大于0两种情况讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值,即可得到函数在相应区间的值域,根据区间[0,2]是A的子集判断出符合这一条件的情况,列出关于a的不等式,求出不等式的解集即可得到满足题意a的取值范围.
解答:解:(1)对函数f(x)求导,f′(x)=
•
.
令f'(x)=0得x=1或x=-1.
当x∈(0,1)时,f'(x)>0,f(x)在(0,1)上单调递增;
当x∈(1,2)时,f'(x)<0,f(x)在(1,2)上单调递减.
又f(0)=0,f(1)=
,f(2)=
,
所以当x∈[0,2],f(x)的值域是[0,
];
(2)设函数g(x)在[0,2]上的值域是A.
∵对任意x1∈[0,2],总存在x0∈[0,2],使f(x1)-g(x0)=0,
∴[0,
]⊆A.
对函数g(x)求导,g'(x)=ax2-a2.
①当a<0时,若x∈(0,2),g'(x)<0,所以函数g(x)在(0,2)上单调递减.
∵g(0)=0,g(2)=
a-2a2<0,
∴当x∈[0,2]时,不满足[0,
]⊆A;
②当a>0时,g′(x)=a(x-
)(x+
).
令g'(x)=0,得x=
或x=-
(舍去).
(i)当x∈[0,2],0<
<2时,列表:
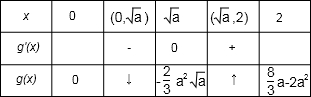
∵g(0)=0,g(
)<0,
又∵[0,
]⊆A,∴g(2)=
a-2a2≥
,解得
≤a≤1.
(ii)当x∈(0,2),
≥2时,g'(x)<0,∴函数在(0,2)上单调递减,
∵g(0)=0,∴g(2)=
a-2a2<0∴当x∈[0,2]时,不满足[0,
]⊆A.
综上,实数a的取值范围是[
,1].
| 4 |
| 3 |
| 1-x2 |
| (x2+1)2 |
令f'(x)=0得x=1或x=-1.
当x∈(0,1)时,f'(x)>0,f(x)在(0,1)上单调递增;
当x∈(1,2)时,f'(x)<0,f(x)在(1,2)上单调递减.
又f(0)=0,f(1)=
| 2 |
| 3 |
| 8 |
| 15 |
所以当x∈[0,2],f(x)的值域是[0,
| 2 |
| 3 |
(2)设函数g(x)在[0,2]上的值域是A.
∵对任意x1∈[0,2],总存在x0∈[0,2],使f(x1)-g(x0)=0,
∴[0,
| 2 |
| 3 |
对函数g(x)求导,g'(x)=ax2-a2.
①当a<0时,若x∈(0,2),g'(x)<0,所以函数g(x)在(0,2)上单调递减.
∵g(0)=0,g(2)=
| 8 |
| 3 |
∴当x∈[0,2]时,不满足[0,
| 2 |
| 3 |
②当a>0时,g′(x)=a(x-
| a |
| a |
令g'(x)=0,得x=
| a |
| a |
(i)当x∈[0,2],0<
| a |

∵g(0)=0,g(
| a |
又∵[0,
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
(ii)当x∈(0,2),
| a |
∵g(0)=0,∴g(2)=
| 8 |
| 3 |
| 2 |
| 3 |
综上,实数a的取值范围是[
| 1 |
| 3 |
点评:此题考查学生会利用导函数的正负得到函数的单调区间,会根据函数的增减性得到函数的极值,灵活运用分类讨论的数学思想,会利用导数求函数的值域,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
,则它是( )
| ||
| |x-3|-3 |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |