题目内容
若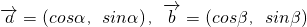 ,,且
,,且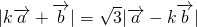 (k>0),
(k>0),
(1)用k表示数量积 ;
;
(2)求 的最小值,并求出此时
的最小值,并求出此时 与
与 的夹角.
的夹角.
解:(1)由已知| |=|
|=| |=1,
|=1,
∵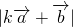 =
=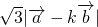 ,
,
∴ ,
,
∴ =
=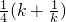 .
.
(2)∵k>0,
∴ ≥
≥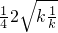 =
= ,
,
∴cosθ= =
= .
.
∴θ=60°.
分析:(1)由已知可得| |=|
|=| |=1,把另一条件平方整理即可,
|=1,把另一条件平方整理即可,
(2)利用均值不等式a+b≥2 求最值,再cosθ=
求最值,再cosθ= 即可求夹角
即可求夹角
点评:如果已知向量的坐标,求向量的夹角,我们可以分别求出两个向量的坐标,进一步求出两个向量的模及他们的数量积,然后代入公式cosθ= 即可求解
即可求解
 |=|
|=| |=1,
|=1,∵
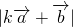 =
=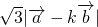 ,
,∴
 ,
,∴
 =
=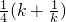 .
.(2)∵k>0,
∴
 ≥
≥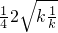 =
= ,
,∴cosθ=
 =
= .
.∴θ=60°.
分析:(1)由已知可得|
 |=|
|=| |=1,把另一条件平方整理即可,
|=1,把另一条件平方整理即可,(2)利用均值不等式a+b≥2
 求最值,再cosθ=
求最值,再cosθ= 即可求夹角
即可求夹角点评:如果已知向量的坐标,求向量的夹角,我们可以分别求出两个向量的坐标,进一步求出两个向量的模及他们的数量积,然后代入公式cosθ=
 即可求解
即可求解 
练习册系列答案
相关题目
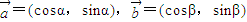 ,,且
,,且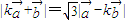 (k>0),
(k>0),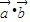 ;
;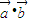 的最小值,并求出此时
的最小值,并求出此时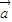 与
与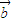 的夹角.
的夹角.