题目内容
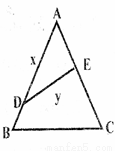
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.(Ⅰ)设AD=x(x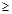 0),ED=y,求用x表示y的函数关系式,并注明函数的定义域;
0),ED=y,求用x表示y的函数关系式,并注明函数的定义域;
(Ⅱ)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?
如果DE是参观线路,则希望它最长,DE的位置又应在哪里?
请给予证明.
【答案】
(Ⅰ)在△ADE中,由余弦定理得:
 ,………………………………………… 1分
,………………………………………… 1分
又 . ‚ …… 2分[来源:
. ‚ …… 2分[来源:
把‚代入得 ,
,
∴ ……………………………………………4分
……………………………………………4分
 ∵
∵  ∴
∴
即函数的定义域为 .…………………………………………… 6分
.…………………………………………… 6分
(Ⅱ)如果DE是水管,则 ,
,
当且仅当 ,即
,即 时“=”成立,故DE//BC,且DE=
时“=”成立,故DE//BC,且DE= .…… 8分
.…… 8分
如果DE是参观线路,记 ,则
,则
∴函数 在
在 上递减,在
上递减,在 上递增
上递增
故 . ……………………………………… 10分
. ……………………………………… 10分
∴ .
.
即DE为AB中线或AC中线时,DE最长
【解析】略

练习册系列答案
相关题目
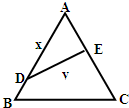 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上. 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.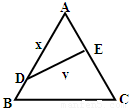 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.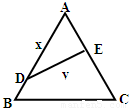 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.