题目内容
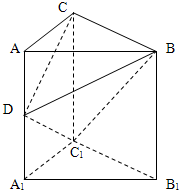 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=1,CC1=2,点D是AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=1,CC1=2,点D是AA1的中点.(1)证明:平面BC1D⊥平面BCD;
(2)求CD与平面BC1D所成角的正切值.
分析:(1)先证明面ABC⊥面ACC1A1,由于AC⊥BC,可得BC⊥面ACC1A1,所以BC⊥C1D,再证明CD⊥C1D,可得C1D?面BC1D,从而可得面BCD⊥面BC1D;
(2)过点C作CH⊥BD交BD于H,可证∠CDH的大小就是CD与平面BC1D所成角的大小,在△CDC1中,可求CD与平面BC1D所成角的正切值.
(2)过点C作CH⊥BD交BD于H,可证∠CDH的大小就是CD与平面BC1D所成角的大小,在△CDC1中,可求CD与平面BC1D所成角的正切值.
解答:(1)证明:∵ABC-A1B1C1为直三棱柱,∴CC1⊥平面ABC,∴面ABC⊥面ACC1A1
由于AC⊥BC,AC=面ABC∩面ACC1A1,∴BC⊥面ACC1A1,∴BC⊥C1D
又∵在矩形ACC1A1中,AA1=2AC,点D是AA1的中点,∴CD⊥C1D.
∵CD∩BC=C,
∴C1D⊥面BCD
∵C1D?面BC1D,
∴面BCD⊥面BC1D--------(7分)
(2)解:过点C作CH⊥BD交BD于H,
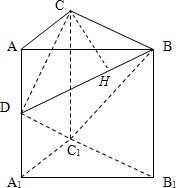
∵平面BC1D⊥平面BCD,面BC1D∩面BCD=BD,∴CH⊥面BC1D.
∴∠CDH就是CD与平面BC1D所成角.--(11分)
在△CDC1中,BC=1,CD=
,
∴tan∠CDH=
=
.-------------(14分)
由于AC⊥BC,AC=面ABC∩面ACC1A1,∴BC⊥面ACC1A1,∴BC⊥C1D
又∵在矩形ACC1A1中,AA1=2AC,点D是AA1的中点,∴CD⊥C1D.
∵CD∩BC=C,
∴C1D⊥面BCD
∵C1D?面BC1D,
∴面BCD⊥面BC1D--------(7分)
(2)解:过点C作CH⊥BD交BD于H,

∵平面BC1D⊥平面BCD,面BC1D∩面BCD=BD,∴CH⊥面BC1D.
∴∠CDH就是CD与平面BC1D所成角.--(11分)
在△CDC1中,BC=1,CD=
| 2 |
∴tan∠CDH=
| 1 | ||
|
| ||
| 2 |
点评:本题考查面面垂直,考查线面角,解题的关键是掌握面面垂直的判定,正确作出线面角,属于中档题.

练习册系列答案
相关题目




